Bài 7: Cho tam giác ABC Â=120, phân giác BD và CE cắt nhau ở O. trên cạnh BC lấy hai điểm I và K sao cho BOI=COK= 30. Chứng minh rằng :
a.OI vuông góc với OK
b. BE+CD<BC
M.ng giải chi tiết giúp mình ạ
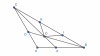
a) Ta có $\widehat{BOC}=180^\circ - \widehat{OBC}-\widehat{OCB} $
$=180^\circ -\dfrac{1}2 \widehat{ABC} -\dfrac{1}2 \widehat{ACB}$
$=180^\circ -\dfrac{1}2 \left(\widehat{ABC}+\widehat{ACB}\right)$
$=180^\circ -\dfrac{1}2 \left(180^\circ-\widehat{BAC} \right)$
$=180^\circ -\dfrac{1}2 \left(180^\circ-120^\circ \right)$
$=150^\circ$
$\implies \widehat{IOK} = \widehat{BOC}-\widehat{BOI}-\widehat{COK}=90^\circ$
Vậy $OI \perp OK$
b) Ta có: $\widehat{BOE}=\widehat{COD}=180^\circ-30^\circ-90^\circ-30^\circ=30^\circ$
Dễ chứng minh được $\triangle BOE =\triangle BOI \quad (g-c-g)$
$\implies BE=BI$
Tương tự chứng minh được $\triangle DCO =\triangle KCO \quad (g-c-g)$
$\implies CD=CK$
$\implies BE+CD=BI+CK$
Mà $BI+CK<BC$
$\implies BE+CD<BC$
Em tham khảo thêm kiến thức khác tại đây nha
https://diendan.hocmai.vn/threads/t...o-ban-hoan-toan-mien-phi.827998/#post-4045397
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
