[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
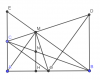
Cho O là trung điểm đoạn thẳng AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm C (khác A), qua O kẻ đường thẳng vuông góc với OC giao By tại D. Kẻ OM vuông CD tại M
a, CM: tam giác OCD ~ tam giác AOC, OM^2 = AC.BD
b, Từ M kẻ MH vuông góc AB tại H. CMR: BC đi qua tđ MH
Giúp mình với!!!!! Mình cảm ơn trước nhé!!!!!!!


a, CM: tam giác OCD ~ tam giác AOC, OM^2 = AC.BD
b, Từ M kẻ MH vuông góc AB tại H. CMR: BC đi qua tđ MH
Giúp mình với!!!!! Mình cảm ơn trước nhé!!!!!!!