mn giúp mình bài 17 này vs ạ , mình cảm ơn nhiều ạ .
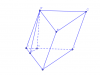
Trong mp' $(BCC'B')$ vẽ $B'H \perp BC=> B'H \perp (ABC)$.
Trong mp' $(ABC)$ từ $H$ vẽ $HD \perp AB$
$=> (\widehat{(ABB'A'),(ABC)})=\widehat{B'DH}=45^o$.
$\Delta B'HD$ vuông cân tại $H$.
Ta có: $HB'=\sqrt{BB'^2-BH^2}=\sqrt{4a^2-BH^2}$(1)
$HD//AC=> \frac{HD}{AC}=\frac{BH}{BC}=> \frac{HB'}{2a.sin60^o}=\frac{BH}{2a}=> HB'=\frac{\sqrt{3}}{2}.BH$(2)
Thay (2) vào (1) $=> \frac{\sqrt{3}}{2}.BH=\sqrt{4a^2-BH^2}=>\frac{7}{4}.BH^2=4a^2=> BH=\frac{4\sqrt{7}}{7}.a$
$=>B'H=\sqrt{4a^2-(\frac{4\sqrt{7}}{7}.a)^2}=\frac{2\sqrt{21}}{7}.a$.
$V=\frac{2\sqrt{21}}{7}.a.\frac{1}{2}.a.2a.sin60^o=\frac{3a^3\sqrt{7}}{7}$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
