[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
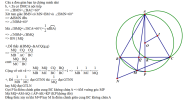
Cho [imath]\triangle ABC[/imath] đều nội tiếp [imath](O)[/imath], đường tròn [imath](I)[/imath] đường kính [imath]AC[/imath] cắt [imath]BC[/imath] ở [imath]K[/imath].
a. Chứng minh: [imath]O, I, K, C[/imath] cùng thuộc một đường tròn
b. Lấy [imath]M \in \overgroup{BC}[/imath], [imath]AM[/imath] cắt [imath]BC[/imath] ở [imath]Q[/imath]. Trên tia đối của tia [imath]MC[/imath] lấy [imath]N[/imath] sao cho [imath]MN = MB[/imath]. Chứng minh:
+ [imath]BN \parallel MQ[/imath]
+ [imath]\dfrac{1}{MQ} = \dfrac{1}{MB} + \dfrac{1}{MC}[/imath]
+ Tìm vị trí của [imath]M[/imath] để [imath]\dfrac{1}{MB} + \dfrac{1}{MC}[/imath] có giá trị nhỏ nhất
Giúp em bài này với ạ, em cảm ơn ạ !
a. Chứng minh: [imath]O, I, K, C[/imath] cùng thuộc một đường tròn
b. Lấy [imath]M \in \overgroup{BC}[/imath], [imath]AM[/imath] cắt [imath]BC[/imath] ở [imath]Q[/imath]. Trên tia đối của tia [imath]MC[/imath] lấy [imath]N[/imath] sao cho [imath]MN = MB[/imath]. Chứng minh:
+ [imath]BN \parallel MQ[/imath]
+ [imath]\dfrac{1}{MQ} = \dfrac{1}{MB} + \dfrac{1}{MC}[/imath]
+ Tìm vị trí của [imath]M[/imath] để [imath]\dfrac{1}{MB} + \dfrac{1}{MC}[/imath] có giá trị nhỏ nhất
Giúp em bài này với ạ, em cảm ơn ạ !
Attachments
Last edited by a moderator:
