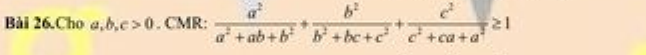Cho [imath]a,b,c>0.[/imath] CMR [imath]\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{c^2+ca+a^2}\ge 1[/imath]
mn giúp e với ạ
truong2008Ta biến đổi bất đẳng thức thành:
[imath]\sum \dfrac{1}{1+\dfrac{b}{a}+\left(\dfrac{b}{a}\right)^2} \geq 1[/imath]
Do [imath]\dfrac{b}{a}.\dfrac{a}{c}.\dfrac{c}{b} =1[/imath], nên ta tồn tại [imath]x,y,z>0[/imath] thỏa mãn:
[imath]\dfrac{b}{a} = \dfrac{yz}{x^2};\dfrac{a}{c}=\dfrac{zx}{y^2} ; \dfrac{c}{b} = \dfrac{xy}{z^2}[/imath]
BĐT cần chứng minh trở thành:
[imath]\dfrac{x^4}{x^4+x^2yz+y^2z^2} + \dfrac{y^4}{y^4+y^2zx+z^2x^2}+\dfrac{z^4}{z^4+z^2xy+x^2y^2} \geq 1[/imath]
Áp dụng bất đẳng thức cộng mẫu, ta có:
[imath]VT \geq \dfrac{(x^2+y^2+z^2)^2}{x^4+x^2yz+y^2z^2+y^4+y^2zx+z^2x^2+z^4+z^2xy+x^2y^2}[/imath]
Nên ta đi chứng minh:
[imath](x^2+y^2+z^2)^2\geq x^4+x^2yz+y^2z^2+y^4+y^2zx+z^2x^2+z^4+z^2xy+x^2y^2[/imath]
[imath]\Leftrightarrow \sum y^2z^2 \geq xyz(x+y+z)[/imath]
Khi này, nếu đặt lại: [imath]yz=m;zx=n;xy=p[/imath], thì ta phải chỉ ra:
[imath]m^2+n^2+p^2 \geq mn+np+pm[/imath] (quen thuộc rồi nha)
Dấu bằng xảy ra khi [imath]x=y=z[/imath]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.