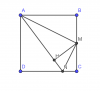
Cho hình vuông ABCD có AB=a. Gọi M là trung điểm của BC, đường thẳng vuông góc vs AM tại M cắt DC tại N. Gọi H là hình chiếu của M trên AN.
a, Chứng minh ▲ABM∾▲MCN
b, Tính giá trị tanMAN
c,Tính giá trị▲AMN theo a
d, Chứng minh 4.AH.AN=5a2
a. Ta có: $\widehat{AMB}+\widehat{NMC}=90^\circ \quad (\widehat{AMN}=90^\circ)$
$\widehat{AMB}+\widehat{BAM}=90^\circ \quad (\Delta ABM)$ vuông
Suy ra $\widehat{BAM}=\widehat{NMC}$
Xét $\Delta ABM$ và $\Delta MCN$ có: $\widehat{ABM}=\widehat{MCN}=90^\circ$; $\widehat{BAM}=\widehat{NMC}$
Suy ra $\Delta ABM \backsim \Delta MCN$ (1)
b. $BM=MC=\dfrac{1}{2}BC=\dfrac{1}{2}a$; $AM=\sqrt{AB^2+BM^2}=\sqrt{a^2+(\dfrac{1}{2}a)^2}=\dfrac{\sqrt{5}}{2}a$
Từ (1) suy ra $\dfrac{AM}{MN}=\dfrac{AB}{MC}\Rightarrow MN=\dfrac{AM.MC}{AB}=\dfrac{\dfrac{\sqrt{5}}{2}a.\dfrac{1}{2}a}{a}=\dfrac{\sqrt{5}a}{4}$
$tanMAN=\dfrac{MN}{AM}=\dfrac{\dfrac{\sqrt{5}a}{4}}{\dfrac{\sqrt{5}}{2}a}=\dfrac{1}{2}$
c. $S_{AMN}=\dfrac{1}{2}AM.MN=\dfrac{1}{2}.\dfrac{\sqrt{5}}{2}a.\dfrac{\sqrt{5}a}{4}=\dfrac{5}{16}a^2$
d. Xét $\Delta AMN$ vuông tại M có MH là đường cao ta có $AH.AN=AM^2=\dfrac{5}{4}a^2\Rightarrow 4AH.AN=5a^2$
Có gì khúc mắc b hỏi lại nhé <3
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
