[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
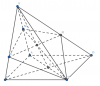
2 ) Cho hình chóp SABCD có đáy là hình bình hành ABCD. Gọi M, N lần lượt là hai điểm thuộc đoạn SA và SB, O là giao điểm của AC và BD.
a/ Tìm giao điểm của (CMN) và đường thẳng SO
b/ Tìm giao tuyến của hai mặt phẳng (SAD) và (CMN)
c/ Tìm thiết diện tạo bởi hình chóp SABCD và (CMN)
a/ Tìm giao điểm của (CMN) và đường thẳng SO
b/ Tìm giao tuyến của hai mặt phẳng (SAD) và (CMN)
c/ Tìm thiết diện tạo bởi hình chóp SABCD và (CMN)