- 21 Tháng bảy 2021
- 9
- 10
- 6
- 19
- Vĩnh Long
- THPT Chuyên Nguyễn Bỉnh Khiêm
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho hình chóp S.ABCD có đáy ABCD là hình thang AD đáy lớn và AD= 2BC. Gọi M,N,P lần lượt thuộc các đoạn sao cho MA=2MS, NA=2ND, PC=2PB
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC); (SAC) và (SBD).
b) Xác định giao điểm Q của SB với mp(MNP).
c) Gọi K trung điểm của SD. Chứng minh CK là giao tuyến của hai mặt phẳng (MQK) và
(SCD).(mình hỏi câu c này)
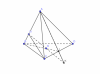
Cho tứ diện ABCD, lấy điểm M trên cạnh AB sao cho AM= 2MB. Gọi G là trọng tâm tam giác BCD, gọi I trung điểm của CD, H là điểm đối xứng của G qua I.
a) Chứng minh GD// (MCH)
b) Tìm giao điểm K của MG với mp(ACD). Tính tỉ số GK/GM(mình hỏi câu b)
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC); (SAC) và (SBD).
b) Xác định giao điểm Q của SB với mp(MNP).
c) Gọi K trung điểm của SD. Chứng minh CK là giao tuyến của hai mặt phẳng (MQK) và
(SCD).(mình hỏi câu c này)
Cho tứ diện ABCD, lấy điểm M trên cạnh AB sao cho AM= 2MB. Gọi G là trọng tâm tam giác BCD, gọi I trung điểm của CD, H là điểm đối xứng của G qua I.
a) Chứng minh GD// (MCH)
b) Tìm giao điểm K của MG với mp(ACD). Tính tỉ số GK/GM(mình hỏi câu b)