[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
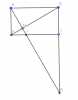
CHO hcn ABCD , AH là đường cao của tam giác ADB và cắt CD ở I. AH cắt BC ở E.
a, CM: [tex]AH^{2}=HI.HE[/tex]
b, Lấy M thuộc BD, kẻ MK vuông góc AB tại K, ME vuông góc AD tại E. CM: MB.MD=EA.ED+KA.KB
a, CM: [tex]AH^{2}=HI.HE[/tex]
b, Lấy M thuộc BD, kẻ MK vuông góc AB tại K, ME vuông góc AD tại E. CM: MB.MD=EA.ED+KA.KB