[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
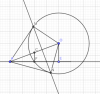
Mọi người cho em hỏi bài này với ạ:Cho điểm O nằm cách đường thẳng a một khoảng 3 cm vẽ đường tròn tâm o bán kính 5 cm.Trên đường thẳng a lấy điểm A nằm ngoài (O).Vẽ tiếp tuyến AM với (O)(M là tiếp điểm).Vẽ dây MN vuông góc OA. chứng minh tâm đường tròn ngoại tiếp tam giác OMN luôn nằm trên 1 đường thẳng cố định