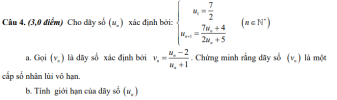[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Câu 4. (3,0 điểm) Cho dãy số [imath]\left(u_{n}\right)[/imath] xác định bởi: [imath]\left\{\begin{array}{l} u_{1}=\dfrac{7}{2} \\ \\ u_{n+1}=\dfrac{7 u_{n}+4}{2 u_{n}+5}\end{array} \quad\left(n \in \mathbb{N}^{*}\right)\right.[/imath]
a. Gọi [imath]\left(v_{n}\right)[/imath] là dãy số xác định bởi [imath]v_{n}=\dfrac{u_{n}-2}{u_{n}+1}[/imath]. Chứng minh rằng dãy số [imath]\left(v_{n}\right)[/imath] là một cấp số nhân lùi vô hạn.
b. Tính giới hạn của dãy số [imath]\left(u_{n}\right)[/imath]
a. Gọi [imath]\left(v_{n}\right)[/imath] là dãy số xác định bởi [imath]v_{n}=\dfrac{u_{n}-2}{u_{n}+1}[/imath]. Chứng minh rằng dãy số [imath]\left(v_{n}\right)[/imath] là một cấp số nhân lùi vô hạn.
b. Tính giới hạn của dãy số [imath]\left(u_{n}\right)[/imath]
Attachments
Last edited:
