Toán 10 Cho $A_{n}$, $B_{n}$ và $C_{n}$_lần lượt là số phần tử của 3 tập $A,B$ và $C$

[zukagm2708]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

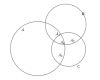
Cho [tex]A_{n}[/tex] , [tex]B_{n}[/tex] và [tex]C_{n}[/tex] lần lượt là số phần tử của 3 tập A, B và C. Giả sử A1 là giao của tập A và B, A2 là giao của tập A và C, A3 là giao của tập B và C, A4 là giao của cả 3 tập A, B và C khi đó hợp của ba tập A, B và C sẽ là: [tex]A\cup B\cup C= A_{n}+B_{n}+C_{n}-A1-A2-A3+A4[/tex]
Bạn hãy chứng minh kết luận trên ! Chúc bạn may mắn

 

[7 1 2 5]

Đây cơ bản là nguyên lí bao hàm loại trừ với trường hợp 3 tập hợp.
Xét sơ đồ Venn như sau:

Từ sơ đồ Venn ta có thể thấy đẳng thức cần chứng minh là hiển nhiên.

Nếu có gì thắc mắc bạn có thể hỏi tại đây, chúng mình luôn sẵn sàng giúp đỡ.
Bạn có thể tham khảo thêm các kiến thức môn học khác tại đây.