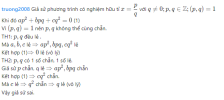Giả sử phương trình có nghiệm hữu tỉ [imath]x= \dfrac{p}{q}[/imath] với [imath]q\ne 0 ; p,q\in \mathbb{Z}; (p,q)=1[/imath]
Khi đó [imath]ap^2 + bpq + cq^2 = 0[/imath] (1)
Vì [imath](p,q)=1[/imath] nên [imath]p,q[/imath] không thể cùng chẵn.
TH1: [imath]p,q[/imath] đều lẻ .
Mà [imath]a,b,c[/imath] lẻ [imath]\Rightarrow ap^2, bpq ,cq^2[/imath] lẻ
Kết hợp (1)[imath]\Rightarrow 0[/imath] lẻ (vô lý)
TH2: [imath]p,q[/imath] có 1 số chẵn, 1 số lẻ.
Giả sử [imath]p[/imath] chẵn, q lẻ [imath]\Rightarrow ap^2 , bpq[/imath] chẵn
Kết hợp (1) [imath]\Rightarrow cq^2[/imath] chẵn.
Mà [imath]c[/imath] lẻ [imath]\Rightarrow q^2[/imath] chẵn [imath]\Rightarrow q[/imath] lẻ (vô lý)
Vậy giả sử sai.
Ngoài ra mời e tham khảo tại [Bài tập] Chuyên đề HSG: Số học
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
