- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào các bạn 
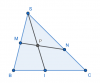
Trong các bài toán về khối đa diện, đôi khi bạn sẽ gặp phải một số biểu thức như $\dfrac{SB}{SM} + \dfrac{SC}{SN} = 2 \cdot \dfrac{SI}{SP}$ nhưng bạn có thể không hiểu là biểu thức đó từ đâu ra. Trong bài viết này mình giới thiệu cho các bạn một công thức khá là hữu ích nhé!
[TBODY]
[/TBODY]
Để nhớ công thức này, bạn cần nhớ hai điều sau:
Cách 1. Sử dụng vector.
Ta có công thức chia điểm: $\vec{SI} = \dfrac{CI}{BC} \vec{SB} + \dfrac{BI}{BC} \vec{SC}$
$\iff BC \cdot \vec{SI} = CI \cdot \vec{SB} + BI \cdot \vec{SC}$
$\iff BC \cdot \dfrac{SI}{SP} \cdot \vec{SP} = CI \cdot \dfrac{SB}{SM} \cdot \vec{SM} + BI \cdot \dfrac{SC}{SN} \cdot \vec{SN}$
Do $P, M, N$ thẳng hàng nên cũng theo công thức chia điểm, ta phải có:
$BC \cdot \dfrac{SI}{SP} = CI \cdot \dfrac{SB}{SM} + BI \cdot \dfrac{SC}{SN}$
Ta có đpcm.
Cách này bạn có thể sử dụng để chứng minh lại công thức mà không cần phải thuộc nhiều.
Cách 2. Sử dụng diện tích.
Mỗi khi thấy tỉ lệ là bạn có thể sử dụng diện tích để chứng minh. Ở đây ta có:
$S_{SMP} + S_{SNP} = S_{SMN}$
$\iff \dfrac{SM \cdot SP}{SB \cdot SI} \cdot S_{SBI} + \dfrac{SN \cdot SP}{SC \cdot SI} \cdot S_{SCI} = \dfrac{SM \cdot SN}{SB \cdot SC} \cdot S_{SBC}$
$\iff \dfrac{SC}{SN} \cdot S_{SBI} + \dfrac{SB}{SM} \cdot S_{SCI} = \dfrac{SI}{SP} \cdot S_{SBC}$
$\iff \dfrac{SC}{SN} \cdot BI + \dfrac{SB}{SM} \cdot CI = \dfrac{SI}{SP} \cdot BC$
Và ta cũng có đpcm
Áp dụng
Thông thường, đề bài sẽ cho các bạn các tỉ lệ cạnh tại $M, N, I$ và mình cần tính tỉ lệ $\dfrac{SP}{SI}$, hoặc đề bài chỉ cho các bạn tỉ lệ tại $I$ và các bạn cần phải tìm sự liên hệ giữa $\dfrac{SB}{SM}$, $\dfrac{SC}{SN}$ và $\dfrac{SP}{SI}$. Trong những trường hợp đó, bạn chỉ cần áp dụng công thức là sẽ ra được ngay nhé
Trong các bài toán về khối đa diện, đôi khi bạn sẽ gặp phải một số biểu thức như $\dfrac{SB}{SM} + \dfrac{SC}{SN} = 2 \cdot \dfrac{SI}{SP}$ nhưng bạn có thể không hiểu là biểu thức đó từ đâu ra. Trong bài viết này mình giới thiệu cho các bạn một công thức khá là hữu ích nhé!
| Cho tam giác $SBC$ như hình vẽ. Gọi $M, N, I$ là các điểm lần lượt nằm trên các cạnh $SB, SC, BC$ và $P$ là giao điểm của $SI$ và $MN$. Khi đó ta có hệ thức sau: $$\dfrac{SB}{SM} \cdot CI + \dfrac{SC}{SN} \cdot BI = \dfrac{SI}{SP} \cdot BC$$ |  |
Để nhớ công thức này, bạn cần nhớ hai điều sau:
- Phần tỉ lệ bị ngược với định lý Ta-lét. Thay vì $\dfrac{SM}{SB}$, ở đây ta có $\dfrac{SB}{SM}$. Nhớ lấy từ đỉnh $S$ hết nhé.
- Các cạnh cũng bị ngược ngược luôn. $SB$ thì nhân $CI$, $SC$ thì nhân với $BI$, $SI$ thì nhân với $BC$.
Cách 1. Sử dụng vector.
Ta có công thức chia điểm: $\vec{SI} = \dfrac{CI}{BC} \vec{SB} + \dfrac{BI}{BC} \vec{SC}$
$\iff BC \cdot \vec{SI} = CI \cdot \vec{SB} + BI \cdot \vec{SC}$
$\iff BC \cdot \dfrac{SI}{SP} \cdot \vec{SP} = CI \cdot \dfrac{SB}{SM} \cdot \vec{SM} + BI \cdot \dfrac{SC}{SN} \cdot \vec{SN}$
Do $P, M, N$ thẳng hàng nên cũng theo công thức chia điểm, ta phải có:
$BC \cdot \dfrac{SI}{SP} = CI \cdot \dfrac{SB}{SM} + BI \cdot \dfrac{SC}{SN}$
Ta có đpcm.
Cách này bạn có thể sử dụng để chứng minh lại công thức mà không cần phải thuộc nhiều.
Cách 2. Sử dụng diện tích.
Mỗi khi thấy tỉ lệ là bạn có thể sử dụng diện tích để chứng minh. Ở đây ta có:
$S_{SMP} + S_{SNP} = S_{SMN}$
$\iff \dfrac{SM \cdot SP}{SB \cdot SI} \cdot S_{SBI} + \dfrac{SN \cdot SP}{SC \cdot SI} \cdot S_{SCI} = \dfrac{SM \cdot SN}{SB \cdot SC} \cdot S_{SBC}$
$\iff \dfrac{SC}{SN} \cdot S_{SBI} + \dfrac{SB}{SM} \cdot S_{SCI} = \dfrac{SI}{SP} \cdot S_{SBC}$
$\iff \dfrac{SC}{SN} \cdot BI + \dfrac{SB}{SM} \cdot CI = \dfrac{SI}{SP} \cdot BC$
Và ta cũng có đpcm
Áp dụng
Thông thường, đề bài sẽ cho các bạn các tỉ lệ cạnh tại $M, N, I$ và mình cần tính tỉ lệ $\dfrac{SP}{SI}$, hoặc đề bài chỉ cho các bạn tỉ lệ tại $I$ và các bạn cần phải tìm sự liên hệ giữa $\dfrac{SB}{SM}$, $\dfrac{SC}{SN}$ và $\dfrac{SP}{SI}$. Trong những trường hợp đó, bạn chỉ cần áp dụng công thức là sẽ ra được ngay nhé