- 16 Tháng tám 2018
- 2,350
- 5,150
- 621
- 20
- Hải Phòng
- THPT Tô Hiệu
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Câu 1.
a. Cho hàm số $y=mx^3+mx^2+(m+1)x-3$. Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên R.
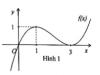
b. Cho hàm số bậc ba $y=f(x)$ có đồ thị như Hình 1. Tìm số giá trị nguyên của m trong đoạn $[-2020;2021]$ để hàm số $h(x)=|f^2(x)+4f(x)-m|$ có đúng 3 điểm cực trị.
Câu 2.
Cho $\log_712=x$, $\log_{12}24=y$ và [tex]\log_{54}168=\frac{axy+1}{bxy+cx}[/tex] trong đó $a;b;c$ là các số nguyên. Tính $S=a+2b+3c$
Câu 3.
Giải phương trình: [tex]\frac{4+cos2x+sin2x-sinx-7cosx}{2sinx+\sqrt{3}}=0[/tex]
Câu 4.
Tìm tất cả các giá trị thực của tham số m để phương trình: [tex]x^3-5x+3+2\sqrt[3]{2x^3-3x^2+m}+m=0[/tex] có đúng 3 nghiệm phân biệt.
Câu 5.
Một bài thi trắc nghiệm có 50 câu hỏi, mỗi câu có 4 phương án và chỉ có duy nhất 1 phương án đúng. Biết mỗi câu trả lời đúng được 0,2 điểm và sai được 0 điểm. Một học sinh không học bài và chọn ngẫu nhiên mỗi câu 1 phương án. Hỏi điểm số nào có xác suất xuất hiện lớn nhất?
Câu 6.
Cho khối tứ diện ABCD. Gọi M;N lần lượt là trung điểm của AB;CD ; P nằm trong BC sao cho BP=k.PC (k>1)
a. Tính thể tích khối tứ diện trong trường hợp tam giác ACD vuông tại A , tam giác BCD vuông cân tại B và AB=AC=AD=a
b. Mặt phẳng đi qua M;N;P chia khối tứ diện thành 2 khối đa diện có thể tích lần lượt và $V_1;V_2$ ( Trong đó $V_1$ là phần thể tích chứa điểm A). Tính [tex]\frac{V_2}{V_1}[/tex]
Câu 7.
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có [tex]\widehat{ACB}=75^o[/tex] , $B(-4;-2)$ ; D thuộc BC sao cho $DC=2DB$ . Biết đường cao kẻ từ A có phương trình $2x+y=0$ và [tex]\widehat{ADC}=60^o[/tex]. Tìm tọa độ của A biết A có hoành độ âm
Câu 8.
Cho các số thực dương a;b;c thay đối .Tìm giá trị nhỏ nhất của biểu thức:
[tex]P=\frac{1}{2\sqrt{2ab}+\sqrt{8bc}}-\frac{2}{\sqrt{2a^2+2b^2+2c^2+4ac}+1}[/tex]
a. Cho hàm số $y=mx^3+mx^2+(m+1)x-3$. Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên R.
b. Cho hàm số bậc ba $y=f(x)$ có đồ thị như Hình 1. Tìm số giá trị nguyên của m trong đoạn $[-2020;2021]$ để hàm số $h(x)=|f^2(x)+4f(x)-m|$ có đúng 3 điểm cực trị.
Cho $\log_712=x$, $\log_{12}24=y$ và [tex]\log_{54}168=\frac{axy+1}{bxy+cx}[/tex] trong đó $a;b;c$ là các số nguyên. Tính $S=a+2b+3c$
Câu 3.
Giải phương trình: [tex]\frac{4+cos2x+sin2x-sinx-7cosx}{2sinx+\sqrt{3}}=0[/tex]
Câu 4.
Tìm tất cả các giá trị thực của tham số m để phương trình: [tex]x^3-5x+3+2\sqrt[3]{2x^3-3x^2+m}+m=0[/tex] có đúng 3 nghiệm phân biệt.
Câu 5.
Một bài thi trắc nghiệm có 50 câu hỏi, mỗi câu có 4 phương án và chỉ có duy nhất 1 phương án đúng. Biết mỗi câu trả lời đúng được 0,2 điểm và sai được 0 điểm. Một học sinh không học bài và chọn ngẫu nhiên mỗi câu 1 phương án. Hỏi điểm số nào có xác suất xuất hiện lớn nhất?
Câu 6.
Cho khối tứ diện ABCD. Gọi M;N lần lượt là trung điểm của AB;CD ; P nằm trong BC sao cho BP=k.PC (k>1)
a. Tính thể tích khối tứ diện trong trường hợp tam giác ACD vuông tại A , tam giác BCD vuông cân tại B và AB=AC=AD=a
b. Mặt phẳng đi qua M;N;P chia khối tứ diện thành 2 khối đa diện có thể tích lần lượt và $V_1;V_2$ ( Trong đó $V_1$ là phần thể tích chứa điểm A). Tính [tex]\frac{V_2}{V_1}[/tex]
Câu 7.
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có [tex]\widehat{ACB}=75^o[/tex] , $B(-4;-2)$ ; D thuộc BC sao cho $DC=2DB$ . Biết đường cao kẻ từ A có phương trình $2x+y=0$ và [tex]\widehat{ADC}=60^o[/tex]. Tìm tọa độ của A biết A có hoành độ âm
Câu 8.
Cho các số thực dương a;b;c thay đối .Tìm giá trị nhỏ nhất của biểu thức:
[tex]P=\frac{1}{2\sqrt{2ab}+\sqrt{8bc}}-\frac{2}{\sqrt{2a^2+2b^2+2c^2+4ac}+1}[/tex]
