[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
NHỊ THỨC NEWTON
1. TAM GIÁC PASCAL
a) Khai triển [imath](a+b)^n, n \in[/imath]{1;2;3;4;5}
Khi khai triển [imath](a+b)^n[/imath], với [imath]n \in[/imath]{1;2;3;4;5} , ta có:[imath](a+b)^1 = a+b[/imath]
[imath](a+b)^2 = a^2 +2ab +b^2[/imath]
[imath](a+b)^3 = a^3+3a^2b+3ab^2+b^3[/imath]
[imath](a+b)^4 = a^4 + 4a^3b + 6a^4b^2 + 4ab^3 +b^4[/imath]
[imath](a+b)^5 = a^5 + 5a^4b + 10a^3b^2 +10a^2b^3 +5ab^4 +b^5[/imath]
Ta có thể dự đoán khai triển của [imath](a+b)^n[/imath], chẳng hạn:
[imath](a+b)^6 =a^6 +? a^5b + ? a^4b^2 + ?a^3b^3 + ? a^2b^4 + ?ab^5 + b^6[/imath]
Dấu “?” chỉ các hệ số chưa biết. Để hoàn thành khai triển, ta cần xác định hệ số này thông qua tam giác Pascal
b) Tam giác Pascal
Khi viết hệ số khai triển [imath](a+b)^n[/imath], với một số giá trị đầu tiên của n gọi là tam giác Pascal: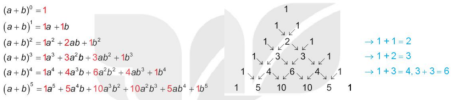
Hàng đầu quy ước là hàng 0. Hàng n ứng với các hệ số trong khai triển nhị thức[imath](a+b)^n[/imath]
Ví dụ 1: Sử dụng tam giác Pascal viết khai triển[imath](a+b)^6[/imath]
Giải
Khai triển [imath](a+b)^6[/imath] có dạng:[imath](a+b)^6 =a^6 +? a^5b + ? a^4b^2 + ?a^3b^3 + ? a^2b^4 + ?ab^5 + b^6[/imath]
Các hệ số trong khai triển là hệ số ở hàng 6 trong tam giác pascal, do vậy, ta có:
Hệ số hàng 6 trong tam giác Pascal là:
Vậy [imath](a+b)^6 =a^6 + 6a^5b + 15a^4b^2 + 20a^3b^3 + 15a^2b^4 + 6ab^5 + b^6[/imath]
Ví dụ 2: Sử dụng tam giác Pascal viết khai triển[imath](3-2x)^5[/imath]
Giải
Dựa vào hàng 5 của tam giác Pascal, ta có:[imath](a+b)^5 = a^5 + 5a^4b + 10a^3b^2 +10a^2b^3 +5ab^4 +b^5[/imath]
Thay a = 3, b= -2x, ta được
[imath](3-2x)^5 = 3^5 + 5.3^4(-2x) + 10.3^3(-2x)^2 +10.3^2(-2x)^3 +5.3(-2x)^4 +(-2x)^5[/imath]
[imath]=243 – 810x +1080x^2 -720x^3 +240x^4 -32x^5[/imath]
c) Tính chất của các số [imath]C^k_n[/imath]
[math]\begin{matrix} (a+b)^1 = a+b=&|&C^0_1a +C^1_1b\\ (a+b)^2 = a^2 +2ab +b^2 =&|& C^0_2a^2 +C^1_2ab + C^2_2b^2 \\ (a+b)^3 = a^3+3a^2b+3ab^2+b^3 =&|&C^0_3a^3 + C^1_3a^2b +C^2_3ab^2+C^3_3b^3 \\ (a+b)^4 = a^4 + 4a^3b + 6a^4b^2 + 4ab^3 +b^4 =&|&C^0_4a^4 + C^1_4a^3b + C^2_4a^4b^2 + C^3_4ab^3 +C^4_4b^4 \\ (a+b)^5 = a^5 + 5a^4b + 10a^3b^2 +10a^2b^3 +5ab^4 +b^5 =&|&C^0_5a^5 + C^1_5a^4b + C^2_5a^3b^2 +C^3_5a^2b^3 +C^4_5ab^4 +C^5_5b^5\end{matrix}[/math]Hệ số khai triển của hai số hạng cách đều số hàng đầu và số hạng cuối luôn bằng nhau
Ví dụ: [imath]C^1_4 = C^3_4 ; C^2_5 = C^3_5; ...[/imath]
Ta có thể viết nhứng hàng đầu của tam giác Pascal dưới dạng:
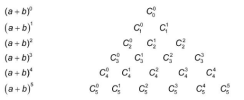
Ta thấy [imath]C^0_1 +C^1_1 =C^1_2 ; C^0_2 +C^1_2 = C^1_3 ; .....[/imath]
