[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨN (2)
Trong phần này, chúng ta sẽ tìm hiểu một số ứng dụng của hệ phương trình bậc nhất ba ẩn và làm quen một số dạng toán giải bằng cách lập hệ phương trình bậc nhất ba ẩn.1. Giải bài toán Vật lí, Hóa học, Sinh học
Ứng dụng trong sinh học:
Ví dụ 1. Một khu rừng ngập mặn có diện tích là 1 ha. Bằng kĩ thuật viễn thám, người ta ước lượng sinh khối trên mặt đất của rừng này là 87,2 tấn/ha. Người ta đếm được trong các ô tiêu chuẩn 100 [imath]m^2[/imath] có tổng số 161 cây trong đó số cây bần bằng 15% tổng số cây mắm và cây đước. Khối lượng trung bình của một cây bần là 10 kg, cây đước là 5 kg và cây mắm là 1 kg. Hãy tính sinh khối của từng loài trên 1 ha rừng.Sinh khối (còn gọi là sinh khối loài) là tổng trọng lượng của sinh vật sống trong sinh quyển hoặc số lượng sinh vật sống trên một đơn vị diện tích.
Giải
Đổi: 87,2 tấn = 87 200 kg: 1 ha = 10 000 [imath]m^2[/imath].Gọi x, y, z theo thứ tự là số cây bần, cây đước và cây mắm trong 1 ha rừng ngập mặn nói trên.
100 [imath]m^2[/imath] có tổng số 161 cây nên 10 000 [imath]m^2[/imath] có số cây là
[imath]161. \frac{10 000}{100} = 16 100[/imath].
Do đó x + y + z = 16 100.
Số cây bần bằng 15% tổng số cây mắm và cây đước nên ta có
[imath]x = \frac{15}{100}(y+z)[/imath]hay 20x-3y-3z=0.
Khối lượng trung bình của một cây bần là 10 kg, cây đước là 5 kg và cây mắm là 1 kg nên ta có
10x+5y + z = 87 200.
Vậy theo bài ra ta có hệ phương trình x+y+z-16 100
[imath]\left\{\begin{matrix} x + y + z = 16 100 \\ 20x-3y-3z-0\\ 10x+5y+ z=87200 \end{matrix}\right.[/imath]
Dùng máy tính cầm tay giải hệ ta được x = 2 100, y = 13 050, z = 950.
Vậy sinh khối bần là 10x = 21 000kg/ha = 21 tấn/ha
Sinh khối đước là: 5y = 65 250kg/ha = 65,25 tấn/ha
Sinh khối mắm là: z = 950 kg/ha = 0,95 tấn/ha
Ứng dụng trong hóa học
Ví dụ 2. Cân bằng phương trình phản ứng quang hợp (dưới điều kiện ánh sáng và chất diệp lục).[imath]CO_{2} + H_{2}O → C_{6}H_{12}O_{6} + O_{2}[/imath]
Giải
Giả sử x, y, z, t là bốn số nguyên dương thoả mãn cân bằng phản ứng[imath]xCO_{2} + yH_{2}O → zC_{6}H_{12}O_{6} + tO_{2}[/imath]
Vì số nguyên tử carbon, hydrogen và oxygen ở hai về phải bằng nhau nên ta có hệ
[imath]\left\{\begin{matrix} x=6z \\ 2y = 12z \\ 2x + y = 6z +2t \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} \frac{x}{t} = 6\frac{z}{t} \\ \frac{y}{t} = 6\frac{z}{t} \\ 2\frac{x}{t} + \frac{y}{t} = 6\frac{z}{t} + 2\end{matrix}\right.[/imath]
Đặt [imath]X =\frac{x}{t}, Y = \frac{y}{t}, Z = \frac{z}{t}[/imath]ta được hệ phương trình bậc nhất ba ẩn
[imath]\left\{\begin{matrix} Y = 6Z \\ X = 6Z \\ 2X + Y = 6Z +2 \end{matrix}\right. hay \left\{\begin{matrix} X-6Z=0 \\ Y-6Z=0 \\ 2X+Y-6Z-2 \end{matrix}\right.[/imath]
Dùng máy tính cầm tay giải hệ ta được X = 1, Y = 1, Z = [imath]\frac{1}{6}[/imath]. Từ đây suy ra x = y= t=6z
Chọn z = 1 ta được x = y = t = 6. Từ đó ta có phương trình cân bằng:
[imath]6CO_{2} + 6H_{2}O → C_{6}H_{12}O_{6} + 6O_{2}[/imath]
Các hệ phương trình bậc nhất xuất hiện trong bài toán cân bằng phản ứng hoá học bao giờ cũng có vô số nghiệm và thường là hệ có trên ba ẩn. Hệ loại này có thể có số ẩn nhiều hơn số phương trình.
Ứng dụng trong vật lí
Ví dụ 3.Cho đoạn mạch ở hình dưới đây. Biết [imath]R_{1}= 25 Ω, R_{2}= 36 Ω, R_{3}= 45 Ω[/imath]và hiệu điện thế giữa hai đầu đoạn mạch U–=60 V. Gọi [imath]I_{1}[/imath] là cường độ dòng điện của mạch chính, [imath]I_{2}[/imath] và[imath]I_{3}[/imath] là cường độ dòng điện mạch rẽ. Tinh [imath]I_{1}, I_{2}, I_{3}[/imath].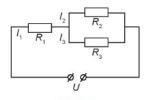
Giải
Từ sơ đồ mạch điện, ta thấy [imath]I_{1}, I_{2}, I_{3}[/imath] là nghiệm của hệ phương trình[imath]\left\{\begin{matrix} I_{1} – I_{2} – I_{3} = 0 \\ R_{1}I_{1} + R_{2}I_{2} = U \\ R_{2}I_{2} - R_{3}I_{3} = 0 \end{matrix}\right. hay \left\{\begin{matrix} I_{1} – I_{2} – I_{3} = 0 \\ 25I_{1} + 36I_{2} = 60 \\ 36I_{1} + 45I_{2} = 0 \end{matrix}\right.[/imath]
Dùng máy tính cầm tay giải hệ, ta được [imath]I_{1} = \frac{4}{3}A, I_{2} = \frac{20}{27}, I_{3} = \frac{16}{27}A[/imath]
2. Giải bài toán cân bằng cung cầu
Các nhà kinh tế học đã chỉ ra rằng, giá cả của một mặt hàng bán trên thị trường phụ thuộc vào ba yếu tố chính.- Thứ nhất, phụ thuộc vào giá trị của bản thân hàng hoá đó.
- Thứ hai, phụ thuộc vào giá trị đồng tiền.
- Thứ ba, phụ thuộc vào quan hệ cung và cầu về mặt hàng đó.
Trong thị trường nhiều mặt hàng, giá cả của mặt hàng này có ảnh hưởng tới giá cả của mặt hàng khác và giá cả của hàng hoá có ảnh hưởng đến lượng cung và lượng cầu của thị trường. Khi phân tích hoạt động của thị trường hàng hoá, các nhà kinh tế học sử dụng hàm cung và hàm cầu đề biểu thị sự phụ thuộc của lượng cung và lượng cầu vào giá cả hàng hoá. Người ta thường phải giải bài toán cân bằng giữa cung và cầu. Bài toán này thường dẫn đến việc giải hệ phương trình bậc nhất nhiều ẩn.
Để đơn giản, ta xét thị trường thực phẩm gồm ba loại mặt hàng là thịt lợn, thịt bò và thịt gà. Khi thịt lợn đắt, thịt bò và thịt gà rẻ thì người tiêu dùng có xu hướng giảm mua thịt lợn, tăng mua thịt bò và thịt gà.
Ví dụ 4. Kí hiệu x,y,z lần lượt là giá 1 kg thịt lợn, 1 kg thịt bò, 1 kg thịt gà (x, y, z >0, đơn vị nghìn đồng)
Kí hiệu : [imath]Q_{S_1} , Q_{S_2}, Q_{S_3}[/imath] lần lượt là lượng thịt lợn, thịt bò, thịt gà người bán chấp nhận với giá x, y và z
[imath]Q_{D_1} , Q_{D_2}, Q_{D_3}[/imath] lần lượt là lượng thịt lợn, thịt bò, thịt gà người mua chấp nhận với giá x, y và z
Cho biết:
| Thịt lợn | Thịt bò | Thịt gà | |||||||
| Hàm Cung | [imath]Q_{S_1} = -120 + 2x[/imath] |
|
| ||||||
| Hàm Cầu |
| [imath]Q_{D_2} = 440 + 2x - y - z[/imath] | [imath]Q_{D_3} = 260 - x - 2y +4z[/imath] |
Hãy giải hệ phương trình cân bằng cung - cầu
Giải
Ta có hệ phương trình cân bằng cung - cầu: [imath]\left\{\begin{matrix} Q_{S_1} = Q_{D_1} \\ Q_{S_2}= Q_{D_2} \\ Q_{S_3} = Q_{D_3} \end{matrix}\right.[/imath] hay [imath]\left\{\begin{matrix} -120 + 2x = 190 -3x+y-z \\ -200 + 2y= 440 + 2x – y - z \\ -210 + 3z = 260 – x – 2y – 4z \end{matrix}\right.[/imath]Thu gọn ta được hệ phương trình:
[imath]\left\{\begin{matrix} 5x – y –z = 310 \\ 2x – 3y – z = -640 \\ x+2y-z = 470 \end{matrix}\right.[/imath]
Dùng máy tính cầm tay giải hệ ta được x = 90; y = 240; z = 100
Vậy giá thịt lợn 90 nghìn đồng\kg, thịt bò 240 nghìn đồng\kg, thịt gà 100 nghìn đồng\kg là hợp lí nhất
BÀI TẬP VẬN DỤNG
Bài 1: Cân bằng phản ứng hóa học sau : [imath]CH_{4} + O_{2} → CO_{2} + H_{2}O[/imath]Bài 2: Trên thị trường có 3 loại sản phẩm A, B, C và giá bán mỗi sản phẩm tương ứng là x,y,z(đơn vị: triệu đồng, x,y,z đều lớn hơn 0) Lượng cung và lượng cầu của mỗi sản phẩm được cho trong bảng dưới đây
Sản phẩm | Lượng Cung | Lượng cầu |
A | [imath]Q_{S_1} = 4x -y - z -5[/imath] | [imath]Q_{D_1} =-2x + y + z + 9[/imath] |
B | [imath]Q_{S_2} = -x +4y - z+5[/imath] | [imath]Q_{D_2} = x - 2y + z +3[/imath] |
C | [imath]Q_{S_3} = -x -y +4z - 1[/imath] | [imath]Q_{D_3} = x+ y -2z -1[/imath] |
Bài 3: Một tuyến cáp treo có ba loại vé sau đây: vé đi lên giá 250 nghìn đồng, vé đi xuống giá 200 nghìn đồng và vé hai chiều giá 400 nghìn đồng. Một ngày, nhà ga cáp treo thu được tổng số tiền là 251 triệu đồng. Tính số vé bán ra mỗi loại, biết rằng nhân viên quản lí cáp treo đếm được 680 lượt người đi lên và 520 lượt người đi xuống.
