Toán 10 [CĐHT Toán 10] ELIP

[JUN._.]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

ELIP​

1. HÌNH DẠNG CỦA ELIP​

​

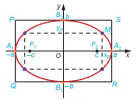
Cho elip có phương trình chính tắc $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ . Khi đó
o Elip có 2 trục đối xứng là Ox và Oy và tâm đối xứng là gốc tọa độ O

o Các điểm $A_1(-a;0)$, $A_2(a;0)$, $B_1(0;-b)$, $B_2(0;b)$ được gọi là các đỉnh
o Đoạn thẳng $A_1A_2$, $B_1B_2$ là trục lớn, trục nhỏ có độ dài lần lượt là 2a và 2b

o $b \leq OM \leq a$ với M thuộc elip
o Hình chữ nhật với 4 đỉnh P(-a; b), Q(-a; -b), R(a; -b), S(a; b) là hình chữ nhật cơ sở của elip

Ví dụ : Cho elip [imath]\dfrac{x^2}{100} + \dfrac{y^2}{25} = 1[/imath]. Tính độ dài các trục và tọa độ các đỉnh của elip

Giải
Các trục lớn, trục nhỏ của elip có độ dài là 2a = [imath]2\sqrt{100}[/imath]=20 và 2b = [imath]2\sqrt{25}[/imath]=10
=>a = 10; b = 5
=> Elip có các đỉnh là [imath]A_1(-10;0)[/imath], [imath]A_2(10;0)[/imath], [imath]B_1(0:-5)[/imath], [imath]B_2(0;5)[/imath]

Chú ý
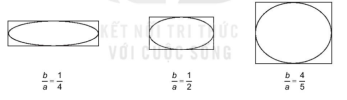
Khi tỉ số [imath]\dfrac{a}{b}[/imath] càng nhỏ( càng gần về 0) thì hình chữ nhật càng “dẹt” và elip càng “gầy”
Khi tỉ số [imath]\dfrac{a}{b}[/imath] càng lớn( càng gần về 1) thì hình chữ nhật càng gần hình vuông và elip càng “béo”