[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
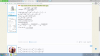
1, Rút gọn: [tex]\frac{\sqrt{\sqrt[4]{8}+\sqrt{\sqrt{2}-1}}-\sqrt{\sqrt[4]{8}-\sqrt{\sqrt{2}-1}}}{\sqrt{\sqrt[4]{8}-\sqrt{\sqrt{2}+1}}}[/tex]
2. CMR: Nếu có [tex]ax^{3}=by^{3}=cz^{3}[/tex] và [tex]\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1[/tex]
thì [tex]\sqrt[3]{ax^2+by^2+cz^2}=\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}[/tex]
3. Cho a= xy+[tex]\sqrt{\left(1+x^2\right)\left(1+y^2\right)}[/tex]
b= [tex]x\sqrt{1+y^2}+y\sqrt{1+x^2}[/tex]
trong đó xy>0. Tính b theo a
4. Cho x,y,z>0 thỏa xy+yz+zx=1
Tính giá trị biểu thức:
P= [tex]x\sqrt{\frac{\left(1+y^2\right)\left(1+z^2\right)}{1+x^2}}+y\sqrt{\frac{\left(1+x^2\right)\left(1+z^2\right)}{1+y^2}}+z\sqrt{\frac{\left(1+y^2\right)\left(1+x^2\right)}{1+z^2}}[/tex]
5. Trục căn: B= [tex]\frac{4}{3+\sqrt{5}+\sqrt{2+2\sqrt{5}}}[/tex]
2. CMR: Nếu có [tex]ax^{3}=by^{3}=cz^{3}[/tex] và [tex]\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1[/tex]
thì [tex]\sqrt[3]{ax^2+by^2+cz^2}=\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}[/tex]
3. Cho a= xy+[tex]\sqrt{\left(1+x^2\right)\left(1+y^2\right)}[/tex]
b= [tex]x\sqrt{1+y^2}+y\sqrt{1+x^2}[/tex]
trong đó xy>0. Tính b theo a
4. Cho x,y,z>0 thỏa xy+yz+zx=1
Tính giá trị biểu thức:
P= [tex]x\sqrt{\frac{\left(1+y^2\right)\left(1+z^2\right)}{1+x^2}}+y\sqrt{\frac{\left(1+x^2\right)\left(1+z^2\right)}{1+y^2}}+z\sqrt{\frac{\left(1+y^2\right)\left(1+x^2\right)}{1+z^2}}[/tex]
5. Trục căn: B= [tex]\frac{4}{3+\sqrt{5}+\sqrt{2+2\sqrt{5}}}[/tex]