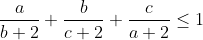Câu 1:
[tex]\dfrac{a}{b^{3}-1}+\frac{b}{a^{3}-1}=\frac{a^{4}-a+b^{4}-b}{(a^{3}-1)(b^{3}-1)}[/tex]
[tex]\dfrac{(a^2+b^2)^2-2a^2b^2-1}{a^3b^3-(a^3+b^3)+1}[/tex]
[tex]=\dfrac{((a+b)^{2}-2ab)^{2}-2a^{2}b^{2}-1}{a^{3}b^{3}-(a+b)(a^{2}-ab+b^{2})+1}[/tex]
[tex]=\dfrac{(1-2ab)^{2}-2a^{2}b^{2}-1}{a^{3}b^{3}-(a+b)^{2}+3ab+1}[/tex]
[tex]=\dfrac{2a^{2}b^{2}-4ab}{a^{3}b^{3}+3ab}[/tex]
[tex]=\dfrac{2(ab-2)}{a^{2}b^{2}+3}[/tex].
Câu 2:
$P \geq 5$ mà P là số nguyên tố nên P sẽ có dạng:$6k-1,6+1$.
Xét P có dạng $6k+1$ khi đó:$2P+1=2(6k+1)+1=12k+3 \vdots 3$.Mà $2P+1$ là số nguyên tố lớn hơn hoặc bằng 5.
Vậy P không thể có dạng $6k+1$.
Xét P có dạng $6k-1$ thì $2P+1$ có thể là số nguyên tố.
Do đó P có dạng $6k+1$ và 2P+1 có dạng $12m-1$.
Khi đó:[tex]2P+2P+1 \\=2(6k-1)+12k-1 \\=12k-2+12k-1 \\=24k-3 \vdots 3[/tex].
Vậy thì rõ ràng $4P+1$ là hợp số.
Từ đó ta có điều phải chứng minh.
Câu 3:
Bạn quy đồng chuyến vế 1 qua ta sẽ được:
[tex]\dfrac{a}{b+2}+\dfrac{b}{c+2}+\dfrac{c}{a+2}-1 \leq 0 \\\Rightarrow \dfrac{a^2c+ab^2+bc^2+2(a^2+b^2+c^2)-abc-8}{(a+2)(b+2)(c+2)} \leq 0 \\\Rightarrow a^2c+ab^2+bc^2+2(a^2+b^2+c^2)-abc-8 \\\Rightarrow a^2c+ab^2+bc^2-2-abc \leq 0[/tex]
do $ a \geq b \geq c$ nên:
[tex]a(a-b)(b-c) \geq 0 \\\Rightarrow (a^2-ab)(b-c) \geq 0 \\\Rightarrow a^2b-a^2c-ab^2+abc \geq 0 \\\Rightarrow a^2c \leq a^2b-ab^2+abc[/tex].
Thay vào trên ta có:
[tex]a^2c+ab^2+bc^2-2-abc \leq a^2b-ab^2+ab^2+abc+bc^2-abc-2 \\=a^2b+bc^2-2 \\DPCM:a^2b+bc^2-2 \leq 0 \\\Rightarrow b(a^2+c^2)-2 \leq 0 \\\Rightarrow b(3-b^2)-2 \leq 0 \\\Rightarrow -(b-1)^2(b+2) \leq 0[/tex]
Điều này hiển nhiên đúng.
Dấu bằng khi $a=b=c=1$.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
=
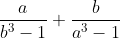}{a^2b^2+3})
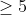thỏa mãn P và 2P+1 là các số nguyên tố.
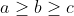và
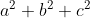=3
