Cần giúp chứng minh hình thang

B

blackmist

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài 1
Tứ giác ABCD(AB=BC=AD). [TEX]\hat{A}=110^o, [/TEX], [TEX]\hat{C}=70^o[/TEX].
a/ Cm DB là phân giác [TEX]\hat{D}[/TEX]
b/ Cm ABCD là hình thang cân

Bài 2
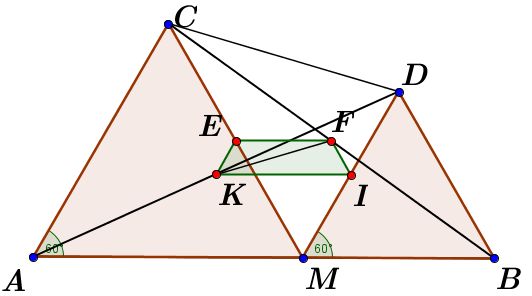
Vẽ điểm M trên đoạn thẳng AB (MA>MB). Trên cùng nmp bờ AB, vẽ các tam giác đều AMC và BMD. E, F, I, K lần lượt là trung điểm của CM, CB, DM, DA.

Chứng minh EFIK là hình thang cân và KF=1/2 CD

P/S: Mình mới vào lớp 8 nên nhiều chỗ chưa hiểu, mong được mọi người giúp đỡ.
 
H

harrypham

untitled-80.jpg

Nhận thấy [TEX]EF [/TEX] là đường trung bình của tam giác [TEX]CMB[/TEX] nên [TEX]EF//MB[/TEX].
[TEX]IK[/TEX] là đường trung bình của tam giác [TEX]DAM[/TEX] nên [TEX]IK//AM[/TEX].
Do đó [TEX]EF//IK[/TEX]. (*)(*)

Ta có [TEX]\widehat{CAM}= \widehat{DMB}=60^o[/TEX] nên [TEX]CA//DM[/TEX], khi đó tứ giác [TEX]CADM [/TEX] là hình thang có [TEX]E,K [/TEX] là trung điểm hai đường chéo nên [TEX]EK//AC[/TEX]. Do đó [TEX]\widehat{CAD}= \widehat{EKD}[/TEX] (đồng vị).
Cũng vì [TEX]KI//AM \Rightarrow \widehat{MAD}= \widehat{IKD}[/TEX] (đồng vị)

Như vậy [TEX]\widehat{CAD}+ \widehat{MAD}= \widehat{EKD}+ \widehat{IKD}[/TEX]
Hay [TEX]\widehat{CAM}= \widehat{EKI}=60^o[/TEX].

Cm tương tự [TEX]\widehat{FIK}= \widehat{DBM}=60^o[/TEX].
Khi đó [TEX]\widehat{EIK}= \widehat{FIK}=60^o[/TEX]. (*)

Từ (*) và (*)(*) ta có tứ giác [TEX]EFIK [/TEX] là hình thang cân.
[TEX]\Rightarrow KF=EI[/TEX].
Mà [TEX]EI[/TEX] là đường trung bình tam giác [TEX]MCD[/TEX] nên [TEX]EI= \frac{1}{2}CD[/TEX] hay [TEX]KF= \frac{1}{2}CD[/TEX].
 
H

harrypham

1. Bài này vẽ hình không khó.
a, Kẻ [TEX]BN \perp AD, BM \perp CD[/TEX].
Xét tam giác vuông [TEX]BNA[/TEX] và [TEX]BMD[/TEX] có
+ [TEX]AB=BC[/TEX]
+ [TEX]\widehat{BAN}= 180^o- \widehat{BAD}=70^o[/TEX] nên [TEX]\widehat{BAN}= \widehat{BCD}=70^o[/TEX].
[TEX]\Rightarrow \triangle BMD= \triangle BND[/TEX] (cạnh huyền - góc nhọn)
[TEX]\Rightarrow BN=BM \Rightarrow BD[/TEX] phân giác góc [TEX]D[/TEX].

b, Nối [TEX]B[/TEX] với [TEX]D[/TEX], do [TEX]AB=AD[/TEX] nên [TEX]\triangle ABD[/TEX] cân ở [TEX]A[/TEX], khi đó [TEX]\widehat{ADB}= \frac{180^o-110^o}{2}=35^o[/TEX].
[TEX]\Rightarrow \widehat{ADC}=70^o[/TEX].

Do [TEX]\widehat{ADC}+ \widehat{BAD}=180^o \Rightarrow AB//CD[/TEX].
Và [TEX]\widehat{BCD}= \widehat{ADC}=70^o[/TEX].
Suy ra tứ giác [TEX]ABCD[/TEX] là hình thang cân.
 
B

blackmist

Không hiểu!!!

Tại sao trung điểm hai đường chéo lại song song với dáy hình thang được??
Làm sao để chứng minh?
Kiến thức này ở đâu ra vậy?
 
H

harrypham

blackmist said:
Tại sao trung điểm hai đường chéo lại song song với dáy hình thang được??
Làm sao để chứng minh?
Kiến thức này ở đâu ra vậy?
Bấm để xem đầy đủ nội dung ...

Sao bạn không thử chứng minh coi: CM một hình thang có đoạn thẳng được tạo bởi trung điểm hai đường chéo sẽ song song với hai đáy và bằng nửa hiệu hai đáy. :)

Mình nghĩ trong một số cuốn sách nâng cao có giới thiệu về tính chất này của hình thang.
 
B

blackmist

Mình chưa gặp cái này bao giờ. Có cách chứng minh nào đơn giản hơn không?
 
You must log in or register to reply here.
Top Bottom