- 16 Tháng một 2019
- 1,420
- 2,113
- 261
- Thanh Hóa
- THCS Nguyễn Du
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
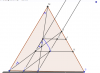
cho ba điểm A,B,C cùng nằm trên đường thẳng D ( C nằm giữa A và B ) trên cùng nửa mặt phẳng bờ D vẽ các tam giác đều AMB và BNC gọi J , Q , K , H thứ tự là trung điểm của BM , CM , BN và AN . chứng minh HQ = 1/2 MN
giúp mình với !!!
giúp mình với !!!