Các đường đồng quy trong tam giác

[angleofdarkness]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Mình có bài toán kèm lời giải sau, bạn nào có lời giải khác (cách làm khác) làm ơn đăng lên dùm mình nha!

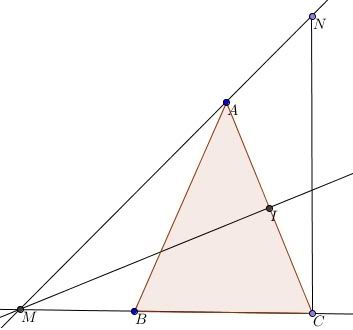
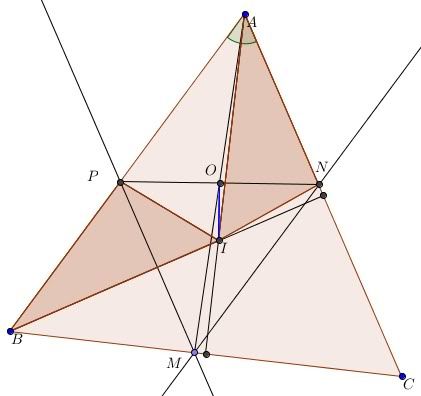
Đề: C/mr trực tâm, trọng tâm và giao ba trung trực tam giác đó nằm trên cùng một đường thẳng.

Gọi H, G, O lần lượt là trức tâm, trọng tâm, giao ba đường trung trực của tam giác ABC và A', B', C' là trung điểm các cạnh BC, AC, CB.
Trên tia đối của OC lấy điểm D sao cho OD = OC.
O, A' là trung điểm DC, BC của tam giác DBC nen OA' là đường trung bình => OA' = BD/2 và OA' // BD.
Mặt khác AH [tex]\perp \[/tex] BC (H là trực tâm tam giác ABC) và OA' [tex]\perp \[/tex] BC (O, A' cách đều B và C).
=> AH // OA'.
=> AH // BD.
C/m tương tự ta có DA // BH.
Vì AH // BD, DA // BH nên AH = BD (t/c đoạn chắn).
Xét tam giác C'BD và tam giác C'AH có:
BD = AH (c/mt).
[tex] \hat{DBC'}[/tex] = [tex] \hat{C'AH}[/tex] (do BA // AH).
C'B = AC' (gt).
=> tam giác C'BD = tam giác C'AH (c.g.c).
=> C'D = C'H; [tex] \hat{DC'B}[/tex] = [tex] \hat{AC'H}[/tex] (hai cạnh; góc tương ứng).
Mà [tex] \hat{AC'H}[/tex] + [tex] \hat{HC'B}[/tex] = [tex] 180^0[/tex] (hai góc kề bù).
=> [tex] \hat{DC'B}[/tex] + [tex] \hat{HC'B}[/tex] = [tex] 180^0[/tex].
=> D, C', H thảng hàng.
C'd = C'H (c/mt0 => C' là trung điểm DH.
Hai tam giác ABC và CDH có chung trung tuyến CC' nên có chung trọng tâm.
G là trọng tâm tam giác ABC => G là trọng tâm tam giác CDH.
HO là đường trung tuyến của tam giác CDH do đó H, G, O thẳng hàng (đpcm).

 

[thaonguyenkmhd]

cái này chứng minh đường thẳng Ơ-le luôn nè bạn..

Cho tam giác ABC Gọi H;G;O là lần lượt là trực tâm, trọng tâm và điểm cách đều 3 đỉnh của tam giác. CMR
a) AH= 2 lần khoảng cách từ 0 đến BC
b) 3 điểm O;H;G thẳng hàng và GH= 2.GO

CHỨNG MINH​

a) Gọi M là trung điểm BC. Lấy điểm D sao cho O là trung điểm CD

Xét [tex]\large\Delta BCD [/tex]có M là trung điểm BC, O là trung điểm CD \Rightarrow OM là đường trung bình của [tex]\large\Delta BCD[/tex]

\Rightarrow [TEX]OM = \frac{1}{2}DB[/TEX] và OM // DB

mà [TEX]OM \bot BC[/TEX] ( OM là đường trung trực của BC ) \Rightarrow [TEX]DB \bot BC[/TEX]

mà [TEX]AH \bot BC[/TEX] ( AH là đường cao của [tex]\large\Delta ABC[/tex] ) \Rightarrow AH // DB

Xét [tex]\large\Delta ABH[/tex] và [tex]\large\Delta BAD[/tex] có

[TEX]\widehat{HAB} = \widehat{DBA}[/TEX] ( 2 góc so le trong do AH // DB )

AB chung

[TEX]\widehat{ABH} = \widehat{BAD}[/TEX] ( 2 góc so le trong do AH // DB )
​

\Rightarrow [tex]\large\Delta ABH = \large\Delta BAD[/tex] ( g-c-g )

\Rightarrow AH = BD mà [TEX]OM = \frac{1}{2}DB[/TEX] \Rightarrow [TEX]OM = \frac{1}{2}AH[/TEX] \Rightarrow [TEX]AH = 2 OM[/TEX] ( đpcm )


b) Gọi G' là giao điển của AM và OH, P là trung điểm G'H, Q là trung điểm G'A

Xét [TEX]\large\Delta[/TEX] AG'H có P là trung điểm G'H, Q là trung điểm G'A \Rightarrow PQ là đường trung bình của [TEX]\large\Delta[/TEX] AG'H

\Rightarrow[TEX] PQ = \frac{1}{2}AH[/TEX] và PQ // AH

Do [TEX] PQ = \frac{1}{2}AH[/TEX] mà [TEX]OM = \frac{1}{2}AH[/TEX] \Rightarrow PQ = OM

Do AH // OM ( cùng [TEX]\bot[/TEX] BC ) mà PQ // AH\Rightarrow PQ // OM

Xét [tex]\large\Delta [/tex] PQG' và [tex]\large\Delta [/tex] OMG' có

[TEX]\widehat{PQG'} = \widehat{OMG'}[/TEX] ( 2 góc so le trong do PQ // OM)

PQ = OM (c/m trên )

[TEX]\widehat{QPG'} = \widehat{MOG'}[/TEX] ( 2 góc so le trong do PQ //OM )
​

\Rightarrow [tex]\large\Delta [/tex] PQG' = [tex]\large\Delta [/tex] OMG' ( g-c-g )

\Rightarrow G'Q = G'M và G'P = G'O

Ta có G'Q = G'M mà G'Q = [TEX]\frac{1}{2}[/TEX]G'A ( Q là trung điểm G'A ) \Rightarrow G'M = [TEX]\frac{1}{2}[/TEX]G'A mà G'M + G'A = AM

\Rightarrow G'A = [TEX]\frac{2}{3}[/TEX] AM mà AM là trung tuyến của [tex]\large\Delta [/tex] ABC

\Rightarrow G' là trọng tâm của [tex]\large\Delta [/tex] ABC ,mà G là trọng tâm của [tex]\large\Delta [/tex] ABC \Rightarrow G' [TEX]\equiv \[/TEX] G

mà G' [TEX]\in[/TEX] OH \Rightarrow G [TEX]\in[/TEX] OH \Rightarrow O, H, G thẳng hàng ( đpcm )

Do G'P = G'O mà G' [TEX]\equiv \[/TEX] G \Rightarrow GP = GO mà GP = [TEX]\frac{1}{2}[/TEX]GH \Rightarrow Go = [TEX]\frac{1}{2}[/TEX]GH \Rightarrow GH= 2GO ( đpcm )

 

[angleofdarkness]

Bài toán sau của mình sẽ khó chơi hơn bài trên, nhờ các bạn giúp nha:

Cho tam giác ABC có AB < AC. M, N, P là trung điểm AB, AC, BC. D, E, F thuộc PC, PB, NA sao cho PD = PM, PE = PN, NF = PE. C/mr MD, NE, PF đồng quy.

 

[angleofdarkness]

Xin giúp mình ba bài này nữa nhé, cảm ơn trước vì các bạn đã ghé qua bài viết:

Bài 1: Cho tam giác ABC cân tại A và đường cao AH. Kẻ HE vuông góc AC. Gọi O là trung điểm EH, I là trung điểm EC. C/mr Ao vuông góc BE.

Bài 2: Cho tam giác ABC cân tại A và cạnh đáy nhỏ hơn cạnh bên. Đường trung trức AC giao BC tại M. Trên tia đối tia AM lấy N sao cho AN = BM.
a) C/m góc AMC = góc BAC.
b) C/m CM = CN.
c) Để Cm vuông góc Cn thì tam gáic ABC cần thêm điều kiện gì.

Bai 3: Cho tam giác ABC đều, M nằm giữa B và C. Biết MP // AC, MN // AB (P thuộc AB, N thuộc AC). C/m:
a) Tam giác BPM và MCN đều.
a) Gọi O là giao điểm Am và PN, I là trọng tâm tam giác ABC. C/mr tam giác IAN = tam giác IBP.
c) Oi là trung trực NP.

 

[hanh99a]

đây chẳng phải là cm đường thẳng ơ-le hay sao bài 1 í phải ko

 

[lovestryno1]

Xin giúp mình ba bài này nhé :
Cho tam giac ABC . Gọi b, c theo thư tư là đường phân giác góc ngoài B.Từ A vẽ các đường thẳng vuông góc với b, c tại M,N
Gọi a là trung trực của IK với I là giao điểm của đường trung trực vuông góc với b và BC , K là giao của đường vuông góc với c và BC.
a, CM : IK bằng chu vi tam giác ABC
b,các đường thẳng a,b,c đồng quy
c,tia Ao là phân giác góc BAC.
Hình mình vẽ đc rồi còn cách làm các bạn cố giúp mình nha .

 

[harrypham]

Bài 2: Cho tam giác ABC cân tại A và cạnh đáy nhỏ hơn cạnh bên. Đường trung trức AC giao BC tại M. Trên tia đối tia AM lấy N sao cho AN = BM.
a) C/m góc AMC = góc BAC.
b) C/m CM = CN.
c) Để Cm vuông góc Cn thì tam gáic ABC cần thêm điều kiện gì.

a) Do $MI$ là đường trung trực của $AC$ nên $MA=MC$, do đó $\triangle AMC$ cân ở $M$.
Hai tam giác $MAC$ và $ABC$ có chung góc $C$ ở đáy nên $\widehat{BAC}= \widehat{AMC}= 180^o - 2 \hat{C}$.

b) Ta có $\widehat{NAC}= \widehat{AMC}+ \widehat{ACB}$ (góc ngoài tam giác $AMC$)
Lại có $\widehat{ABM}= \widehat{BAC}+ \widehat{ACB}$
Mà $\widehat{AMC}= \widehat{BAC}$ (câu a) nên $\widehat{NAC}= \widehat{AMC}$
$\implies \triangle ABM = \triangle CAN \; ( \text{ c.g.c})$
$\implies CM=CN (=AM)$.

c) Nếu $CM \perp CN$ thì $\triangle MCN$ vuông cân ở $C$.
$\implies \widehat{AMC}= \widehat{BAC}=45^o$.

 

[harrypham]

Bai 3: Cho tam giác ABC đều, M nằm giữa B và C. Biết MP // AC, MN // AB (P thuộc AB, N thuộc AC). C/m:
a) Tam giác BPM và MCN đều.
a) Gọi O là giao điểm Am và PN, I là trọng tâm tam giác ABC. C/mr tam giác IAN = tam giác IBP.
c) Oi là trung trực NP.

a) Ta có $\widehat{BAC}= \widehat{BPM}= \widehat{MNC}=60^o$ (đồng vị)
Và $\widehat{ABC}= \widehat{ACB}=60^o$
Nên hai $\triangle BPM$ và $\triangle MNC$ đều (do có hai góc bằng $60^o$)

b) Trong tam giác đều, trọng tâm cũng chính là giao của ba đường phân giác trong tam giác, giao của ba đường trung trực của mỗi cạnh tam giác.

Do đó $IA=IB$ ($I$ thuộc đường trung trực của $AB$) và $\widehat{IAN}= \widehat{IBP}=30^o$ ($I$ là giao điểm ba đường phân giác của tam giác).

Ta có $AP//MN, \; MP//AN$ nên theo tính chất đoạn chắn thì $AN=PM=BP$.
Như vậy $\triangle IPB= \triangle INA \; (\text{c.g.c})$

c) Từ $\triangle IPB= \triangle INA \implies IP=IN \implies I$ thuộc đường trung trực của $PN$, mà $O$ trung điểm $PN$ nên $OI$ là đường trung trực của $PN$. $\square$