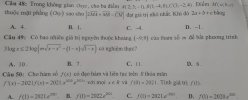[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Câu 48: Trong không gian [imath]O x y z[/imath], cho ba điểm [imath]A(2 ; 3 ;-1), B(1 ;-4 ; 0), C(3 ;-2 ; 4)[/imath]. Điểm [imath]M(a ; b ; c)[/imath] thuộc mặt phẳng [imath](O x y)[/imath] sao cho [imath]|2 \overrightarrow{M A}+\overrightarrow{M B}-\overline{C M}|[/imath] đạt giá trị nhỏ nhất. Khi đó [imath]2 a+b+c[/imath] bằng
A. 4 .
B. 1 .
C.-4.
D.-1.
Câu 49: Có bao nhiêu giá trị nguyên thuộc khoảng [imath](-9 ; 9)[/imath] của tham số [imath]m[/imath] để bất phương trình [imath]3 \log x \leq 2 \log \left(m \sqrt{x-x^{2}}-(1-x) \sqrt{1-x}\right)[/imath] có nghiệm thực?
A. 10 .
B. 7 .
C. 11 .
D. 6 .
Câu 50: Cho hàm số [imath]f(x)[/imath] có đạo hàm và liên tục trên [imath]R[/imath] thỏa mãn [imath]f^{\prime}(x)-2021 f(x)=2021 \cdot x^{2020} \cdot e^{2021 x}[/imath] với mọi [imath]x \in R[/imath] và [imath]f(0)=2021[/imath]. Tính giá trị [imath]f(1)[/imath].
A. [imath]f(1)=2021 \cdot e^{2021}[/imath].
B. [imath]f(1)=2022 \cdot e^{2021}[/imath].
C. [imath]f(1)=2021 \cdot e^{-2021}[/imath].
D. [imath]f(1)=2020 \cdot e^{2021}[/imath].
Giúp em ba câu này với ạ @chi254 @Timeless time
A. 4 .
B. 1 .
C.-4.
D.-1.
Câu 49: Có bao nhiêu giá trị nguyên thuộc khoảng [imath](-9 ; 9)[/imath] của tham số [imath]m[/imath] để bất phương trình [imath]3 \log x \leq 2 \log \left(m \sqrt{x-x^{2}}-(1-x) \sqrt{1-x}\right)[/imath] có nghiệm thực?
A. 10 .
B. 7 .
C. 11 .
D. 6 .
Câu 50: Cho hàm số [imath]f(x)[/imath] có đạo hàm và liên tục trên [imath]R[/imath] thỏa mãn [imath]f^{\prime}(x)-2021 f(x)=2021 \cdot x^{2020} \cdot e^{2021 x}[/imath] với mọi [imath]x \in R[/imath] và [imath]f(0)=2021[/imath]. Tính giá trị [imath]f(1)[/imath].
A. [imath]f(1)=2021 \cdot e^{2021}[/imath].
B. [imath]f(1)=2022 \cdot e^{2021}[/imath].
C. [imath]f(1)=2021 \cdot e^{-2021}[/imath].
D. [imath]f(1)=2020 \cdot e^{2021}[/imath].
Giúp em ba câu này với ạ @chi254 @Timeless time
Attachments
Last edited by a moderator: