Các bài toán hay và khó tổng hợp----cần giúp đỡ!

[hhai2002]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Câu 1: Chứng minh rằng
10^150+5*10^50+1 không là lập phương của một số tự nhiên
Câu 2: Cho a+b+c=0. Chứng minh rằng
a) M=N=P với
M=a(a+b)(a+c) N=b(b+c)(b+a) P=c(c+a)(c+b)
b)a^4+b^4+c^4=2(a^2*b^2+b^2*c^2+c^2*a^2)
c)a^4+b^4+c^4=2(ab+bc+ca)^2
d)a^4+b^4+c^4=\frac{(a^2+b^2+c^2)^2}{2}
Câu 3:Cho
(x^2+y^2)/(x^2-y^2)+(x^2-y^2)/(x^2+y^2)=k
Tính A theo k
A={x^8+y^8}/{x^8-y^8}+{x^8-y^8}/{x^8+y^8}
Câu 4: Tìm ƯCLN của các số A(n)=2^(3n)+3^(6n+2)+5^(6n+2) với n\leq1999
Câu 5: Tìm các số nguyên x và y biết
(x+1)(x+2)(x+3)+x(x+2)(x+3)+x(x+1)(x+3)+x(x+1)(x+2)=y^(2^x)
Câu 6: Có bao nhiêu số chính phương mà 2 chữ số cuối giống nhau?
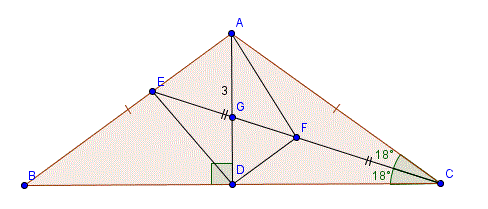
Câu 7: Cho tam giác ABC cân tại A, AD vuông góc BC. E thuộc AB sao cho \{ACE}=\{ECB}=18. Giả sử AD=3 cm, tìm độ dài CE

 

[soccan]

$1\\
A=10^{150}+5.10^{50}+1$
có $4|10^2$ nên $4|10^{150}$ và $4|10^{50}$
do đó $A \equiv 5+1 \equiv\ 2\ (mod\ 4)$
nên $A$ không là lập phương của $1$ số tự nhiên

 

[iceghost]

Câu 7

Gọi G là giao điểm ED và AD

Xét $\triangle$ ABC cân tại A có :
AD là đường cao
\Rightarrow AD là đường trung tuyến
\Rightarrow D là trung điểm BC
Gọi F là trung điểm của EC
Ta có : FD là đường trung bình của $\triangle$ EBC
\Rightarrow FD // EB hay AB

Xét $\triangle$ ABC có
$\hat{C} = \hat{B} = 18^o + 18^o = 36^o$ ( $\triangle$ ABC cân )
Mà $\widehat{AEF} = 180^o - \widehat{BEC} = 180^o - (180^o - \widehat{ECB} - \hat{B})$
\Rightarrow $\widehat{AEF} = 180^o - (180^o - 18^o - 36^o) = 180^o - 126^o = 54^o$
Mà $\widehat{EAD} = 90^o - \hat{B} = 90^o - 36^o = 54^o$
\Rightarrow $\widehat{EAD} = \widehat{AEF}$
\Rightarrow $\triangle$ EAG cân tại G
\Rightarrow AG = EG (1)

Ta có : $\widehat{EAD} = \widehat{ADF}$ ( so le trong )
$\widehat{AEF} = \widehat{EFD}$ ( so le trong )
Mà $\widehat{EAD} = \widehat{AEF}$ (cmt)
\Rightarrow $\widehat{ADF} = \widehat{EFD}$
\Rightarrow $\triangle$ GDF cân tại G
\Rightarrow GD = GF (2)

Cộng (1) vào (2) ta có :
AG + GD = EG + GF
AD = EF
3 cm = $\frac{1}{2} EC$
Vậy EC = 6 cm

 

[trucphuong02]

Câu 2

a> Theo đề bài, ta có: a+b+c=0
a+b= -c
\Rightarrow a+c= -b
b+c= -a
Ta có:
* M=a.(a+b).(a+c)
\Rightarrow M=a.(-c).(-b) (1)
* N=b(b+c)(b+a)
\Rightarrow N= b.(-a).(-c) \Rightarrow N= a.(-c).(-b) (2)
* P= c.(c+a).(c+b)
\Rightarrow P= c.(-b).(-a) \Rightarrow P= a.(-c).(-b) (3)
Từ (1);(2) và (3)
\Rightarrow M=N=P

b> Theo đề bài, ta có: a+b+c=0 \Rightarrow b+c= -a
\Rightarrow $(b+c)^2$ = $(-a)^2$
\Rightarrow $b^2$ + $c^2$ + 2bc = $a^2$
\Rightarrow $b^2$ + $c^2$ - $a^2$ = -2bc
\Rightarrow $ ( $b^2$ + $c^2$ - $a^2$ )^2 $ = $(-2bc)^2$
\Rightarrow $a^4$ + $ b^4$ + $c^4$ + 2 $b^2$ $c^2$ -2 $a^2$ $b^2$ - 2 $a^2$ $c^2$ = 4 $b^2$ $c^2$
\Rightarrow $a^4$ + $ b^4$ + $c^4$ = -2 $b^2$ $c^2$ + 2 $a^2$ $b^2$ + 2 $a^2$ $c^2$ + 4 $b^2$ $c^2$
\Rightarrow $a^4$ + $ b^4$ + $c^4$ = 2 $b^2$ $c^2$ + 2 $a^2$ $b^2$ + 2 $a^2$ $c^2$
\Rightarrow $a^4$ + $ b^4$ + $c^4$ =2.($a^2$ $b^2$ + $b^2$ $c^2$ + $a^2$ $c^2$)

 

[soccan]

$2)\\
c)\ (ab+bc+ca)^2=a^2b^2+c^2a^2+c^2b^2+2abc(a+b+c)=a^2b^2+b^2c^2+a^2c^2$
mà $a^4+b^4+c^4=2(a^2b^2+b^2c^2+a^2c^2)$ (câu $b$)
$d)\ \dfrac{(a^2+b^2+c^2)^2}{2}=\dfrac{a^4+b^4+c^4+2(a^2b^2+c^2a^2+b^2c^2)}{2}$
sử dụng câu $b$ ta có điều cần chứng minh