BT violimpic vòng 4

[kienduc_vatli]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

1, Cho tam giác ABC vuông tại A, đường phân giác trong BD = $6\sqrt{5}$ cm và 5DA = 3DC. Khi đó BC = cm.
2.

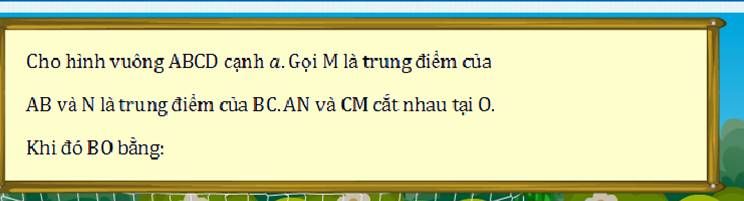
3.

cách làm rõ ràng nhé!

 

[transformers123]

Bạn tự vẽ hình nhá =)):

Gọi $DE \bot AB$, $DF \bot AC$

Dễ dàng chứng minh $\Delta AED$ cân tại $E\ \rightarrow DE=\dfrac{AD\sqrt{2}}{2}$ (dùng Pi-ta-go)

Dễ dàng chứng minh $\Delta AFD$ cân tại $F\ \rightarrow DF=\dfrac{AD\sqrt{2}}{2}$ (dùng Pi-ta-go)

Ta có:

$S_{ABD}+S_{ACD}=S_{ABC}$

$\Longrightarrow \dfrac{DE.AB}{2}+\dfrac{DF.AC}{2}=\dfrac{AB.AC}{2}$

$\Longrightarrow \dfrac{AB.AD\sqrt{2}}{2}+\dfrac{AC.AD\sqrt{2}}{2}=\dfrac{AB.AC}{2}$

$\Longrightarrow \dfrac{AD}{\sqrt{2}}(AB+AC)=\dfrac{AB.AC}{2}$

$\Longrightarrow \dfrac{\sqrt{2}}{AD}=\dfrac{AB+AC}{AB.AC}$

$\Longrightarrow \dfrac{\sqrt{2}}{AD}=\dfrac{1}{AB}+\dfrac{1}{AC}$

.........

 

[trinhminh18]

Câu 2: dễ dàng c/m $\Delta{ABN}=\Delta{CBM}$
\Rightarrow $\widehat{BAN}=\widehat{BCM}$
tam giác AMO và tam giác ONC có $\widehat{BAN}=\widehat{BCM}$ và 2 góc đối đỉnh = nhau nên $\widehat{AMO}=\widehat{ONC}$
\Rightarrow $\Delta{AMO}=\Delta{CNO}$
\Rightarrow AO=CO
\Rightarrow $\Delta{ABO}=\Delta{CBO}$
\Rightarrow BO là phân giác góc ABN
\Rightarrow $\dfrac{NO}{AO}=\dfrac{BN}{AB}= \dfrac{1}{2}$
MẶt kháC $\dfrac{NO}{AO}= \dfrac{BO}{DO}$ (đ lý ta-lét)
\Rightarrow $DO=2BO$
MÀ $BO+ DO= BD =\sqrt{BC^2+DC^2} =\sqrt{2a^2}= a\sqrt{2}$ (pytago)
\Rightarrow $3BO=a\sqrt{2}$ \Rightarrow $BO=\dfrac{a\sqrt{2}}{3}$