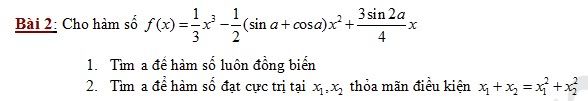BT về cực trị ???

[huy8687]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Các bạn giải giùm mình câu 1 nhé !!

 

[connguoivietnam]

a)
[TEX]y=f(x)=\frac{1}{3}x^3-\frac{1}{2}(sina+cosa)x^2+\frac{3sin2a}{4}x[/TEX]

[TEX]y'=x^2-(sina+cosa)x+\frac{3sin2a}{4}[/TEX]

để hàm số đồng biến trên R thì [TEX]y' \geq 0[/TEX]

[TEX]x^2-(sina+cosa)x+\frac{3sin2a}{4} \geq 0[/TEX]

[TEX]4x^2-4(sina+cosa)x+3sin2x \geq 0[/TEX]

[TEX]4(sina+cosa)^2-12sin2x \leq 0[/TEX]

b)
[TEX]x_{1}+x_{2}=x^2_{1}+x^2_{2}[/TEX]

[TEX]x_{1}+x_{2}=(x_{1}+x_{2})^2-2x_{1}x_{2}[/TEX]

[TEX]y'=x^2-(sina+cosa)x+\frac{3sin2a}{4}[/TEX]

để pt có [TEX]x_{1}[/TEX] và [TEX]x_{2}[/TEX] thì

[TEX](sina+cosa)^2-3sin2a \geq 0[/TEX]

áp dụng vi-ét

[TEX]x_{1}+x_{2}=sina+cosa[/TEX]

[TEX]x_{1}x_{2}=\frac{3sin2a}{4}[/TEX]

[TEX]sina+cosa=1+sin2a-\frac{3sin2a}{2}[/TEX]

giải pt lượng giác là ra a thôi bạn ạ

 

[huy8687]

a)
[TEX]y=f(x)=\frac{1}{3}x^3-\frac{1}{2}(sina+cosa)x^2+\frac{3sin2a}{4}x[/TEX]

[TEX]y'=x^2-(sina+cosa)x+\frac{3sin2a}{4}[/TEX]

để hàm số đồng biến trên R thì [TEX]y' \geq 0[/TEX]

[TEX]x^2-(sina+cosa)x+\frac{3sin2a}{4} \geq 0[/TEX]

[TEX]4x^2-4(sina+cosa)x+3sin2x \geq 0[/TEX]

[TEX]4x^2-4(sina+cosa)x+(sina+cosa)^2-1-sin2a+3sin2x \geq 0[/TEX]

[TEX](2x-sina-cosa)^2-1-sin2a+3sin2x \geq 0[/TEX]

vậy [TEX]3sin2x-sin2a-1 \geq 0[/TEX]

[TEX]3 \geq 3sin2x \geq -3[/TEX]

[TEX]2 \geq (sina+cosa)^2 \geq 0[/TEX]

b)
[TEX]x_{1}+x_{2}=x^2_{1}+x^2_{2}[/TEX]

Nếu nó đồng biến thì y' > 0 thì sao bạn ko dùng delta \leq 0 và a>0
thế hay hơn đó

 

[lantrinh93]

thế này ,muốn y ' >0 ,mà y' là hàm bậc 2 thì[TEX]\Delta\[/TEX]<và a>0 vì
+ [TEX]\Delta\[/TEX] < 0 để phương trình bậc hai vô nghiệm
\Rightarrow khi lập bảng xét dấu thì ta phải xét Y' cùng dấu với a
vì a> 0 nên bảng xét dấu toàn là dấu toàn là dấu +
\Rightarrow hàm đồng biến
ôi,tớ đang buồn ngủ ,thông cảm ,giải thích không được logic cho lắm

 

[trang.160493]

thế này ,muốn y ' > 0 ,mà y' là hàm bậc 2 thì[TEX]\Delta\[/TEX]<và a>0 vì
+ [TEX]\Delta\[/TEX] < 0 để phương trình bậc hai vô nghiệm
\Rightarrow khi lập bảng xét dấu thì ta phải xét Y' cùng dấu với a
vì a> 0 nên bảng xét dấu toàn là dấu toàn là dấu +
\Rightarrow hàm đồng biến
ôi,tớ đang buồn ngủ ,thông cảm ,giải thích không được logic cho lắm

uh, cách của lantrinh được sử dụng nhiều đó. cô jáo mìh khuyên nên làm theo cách đó cho nó gọn
Hsố đbiến \Leftrightarrow y' \geq 0 \Leftrightarrow[TEX]\Delta\[/TEX] \leq 0 và a > 0