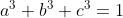1, Cho xyz=1 và
.Tính
2,Cho a+b+c=1;
;
Tính
3,Tìm tất cả chữ số có 5 chữ số abcde sao cho :
1.
Từ gt suy ra $x+y+z=xy+yz+zx$
$\Rightarrow xy- yz - zx + x + y + z = 0$
$\Rightarrow xyz - xy - yz - zx + x + y + z - 1 = 0$
$\Leftrightarrow (x - 1)(y - 1)(z - 1) = 0$
Suy ra trong $3$ số $x,y,z$ có ít nhất một số $=1$ suy ra $P=0$
2.
Từ gt ta có $-1\leq a,b,c\leq 1\Rightarrow a-1;b-1;c-1\leq 0$
$\Rightarrow a^{2}(a-1)\leq 0;b^{2}(b-1)\leq 0;c^{2}(c-1)\leq 0$
Mà $a^{3}+b^{3}+c^{3}=a^{2}+b^{2}+c^{2}\Rightarrow a^{2}(a-1)+b^{2}(b-1)+c^{2}(c-1)=0$
$\Rightarrow a^{2}(a-1)=b^{2}(b-1)=c^{2}(c-1)=0\Rightarrow a,b,c$ nhận hai giá trị là 0 or 1
$\Rightarrow b^{2012} = b^2; c^{2013} = c^2\Rightarrow S = a^2 + b ^{2012} + c^{2013} = 1$
3.
gt $\Rightarrow \overline{abcde}=\overline{ab}^3$ $(22\leq \overline{ab}\leq 46)$
$\overline{ab}^3-\overline{abcde}=0\Leftrightarrow \overline{ab}^3-1000\overline{ab}=\overline{cde}\Leftrightarrow \overline{ab}(\overline{ab}^2-1000)=\overline{cde}$
Mà $100\leq \overline{cde}\leq 999;22\leq \overline{ab}\leq 46\Rightarrow 3\leq \overline{ab}^2-1000\leq 45$
Suy ra $1003\leq \overline{ab}^2\leq 1045\Leftrightarrow 31<\overline{ab}\leq 32\Rightarrow \overline{ab}=32$
Vậy số có $5$ chữ số cần tìm là $32^3=32768$
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
.Tính
(y^{5}-1)(z^{1890}-1))
;
