Toán 9 BT ĐƯỜNG TRÒN ( HK1)

[Suga Min Yoongi]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

GIÚP EM CÂU C VỚI D THÔI Ạ.

1)
Cho nửa đường tròn (O;R), đường kính AB. Lấy M thuộc (O). Tiếp tuyến tại M của (O) cắt tiếp tuyến tại A và B lần lượt tại C và D. Kẻ đường cao MH trong ΔAMB.
a) Cm: AC + BD = CD
b) Cm: góc COD = 90° suy ra AC.BD = R^2
c) Cm: MH.CD không đổi
d) Cm: KM là phân giác góc CKD

2)
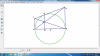
Cho đường tròn tâm O, đường kính AB = 2R. Lấy F ∈ (O), tiếp tuyến tại F cắt 2 tiếp tuyến tại A và B của (O) lần lượt tại C, D.
a) Cm: Δ COD vuông
b) Cm: CD = AC + BD. Cm: AC.BD = R^2
c) Từ F vẽ FH vuông góc với AB tại H. Cm: BC đi qua trung điểm FH.
d) Vẽ (F,FH) cắt (O) tại I, E. Cm: IE, FH, BC đồng qui

 

[candyiukeo2606]

1.

c,
Gọi G là giao điểm của AD và BC => $\frac{AC}{BD} = \frac{CG}{BG} = \frac{CM}{MD}$ => $\frac{CG}{BC} = \frac{CM}{CD}$ => MG // BD
Mà MH // BD => M, H, G thẳng hàng
Vì MG // BD => $\frac{MG}{BD} = \frac{CM}{CD} = \frac{AH}{AB}$ (1)
Vì HG // BD => $\frac{HG}{BD} = \frac{AH}{AB}$ (2)
(1), (2) => MG = HG
Ta có: $\frac{MG}{BD} = \frac{CM}{CD} = \frac{MH}{2MD} = \frac{CM}{CD}$
=> $CD = \frac{2MD.MC}{MH} = \frac{2R^2}{MH}$
=> $MH.CD = 2R^2$ -> không đổi
d,
Vì $\frac{CM}{MD} = \frac{AH}{BH}$ => $\frac{AC}{BD} = \frac{AH}{BH}$
Có tỉ số, $\widehat{CAH} = \widehat{DBH} = 90^o$
=> [tex]\Lambda CAH \sim DBH \Rightarrow \widehat{AHC} = \widehat{BHD} \Rightarrow \widehat{MHC} = \widehat{MHD}[/tex]
=> CM là phân giác $\widehat{CHD}$
2.c bạn xem lại câu 1.c mình vừa giải :3