H
hanhdungpro
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
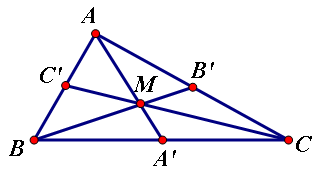
Cho $M$ ở miền trong tam giác $ABC$. Các đường thẳng $AM, BM, CM$ cắt các cạnh $BC, CA, AB$ lần lượt tại $A', B', C'$. Tính $\dfrac{AM}{AA'}+\dfrac{BM}{BB'}+\dfrac{CM}{CC'}$
_______________________________________________________________________
Thứ 5 mình cần. ai giải giúp mình nha. cảm ơn nhiều
_______________________________________________________________________
Thứ 5 mình cần. ai giải giúp mình nha. cảm ơn nhiều
Last edited by a moderator: