- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài toán biện luận m để số nghiệm của phương trình f(x)=0 thỏa mãn đề cho, có 2 trường hợp khả dĩ:
1. Pt có nghiệm x=a cố định với mọi m, thì ta cố gắng phân tích f(x)=(x-a)g(x) với g(x) là đa thức bậc 2, từ đó dùng delta để biện luận số nghiệm thỏa mãn
2. PT không có các nghiệm cố định, ta cố gắng cô lập m và x. Từ đó đưa về PT g(x)=m. Khảo sát vẽ BBT của g(x), số nghiệm pt g(x)=m chính bằng số giao điểm đường thẳng nằm ngang y=m và g(x)
Các bài toán phân tích được nhân tử đã được nêu ở đây , nên ở đây chỉ nêu về các bài toán cô lập.
1. Biện luận theo m để số nghiệm của phương trình [TEX]x^2-3x-m=0(1)[/TEX]
Lời giải: ta có [tex](1)<=>x^2-3x=m[/tex]
Khảo sát hàm [TEX]f(x)=x^3-3x[/TEX] , ta có [TEX]f'(x)=3x^2-3;f'(x)=0<=>x=-1;x=1[/TEX]
Từ đó ta lập được BBT và suy ra được dạng đồ thị của hàm f(x) như sau:
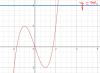
Từ đồ thị ta thấy, với m>2 hoặc m<-2 thì pt đã cho có nghiệm duy nhất
Với m=2 hoặc m=-2 thì pt đã cho có 2 nghiệm, trong đó có 1 nghiệm kép
Với -2<m<2 thì pt đã cho có 3 nghiệm phân biệt.
2. Tìm m để pt : [TEX]x^3+x^2(m+1)+3x+m=0[/TEX](1) có 3 nghiệm phân biệt.
Để cô lập được ta phải nhóm các số hạng có chứa m vào với nhau:
(1)<=>[tex]x^3+x^2+3x+m(x^2+1)=0<=>m=\frac{-(x^3+x^2+3x)}{x^2+1}[/tex]
Khảo sát hàm [TEX]f(x)=\frac{-(x^3+x^2+3x)}{x^2+1}[/TEX]
Ta có: [tex]f'(x)=-\frac{x^4+2x+3}{(x^2+1)^2}[/tex] , ta thấy [TEX]f'(x)<0[/TEX] với mọi x, do đó hàm f(x) NB trên R
Vậy ta có đồ thị f(x) như sau :
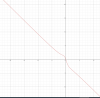
Vậy pt đã cho luôn chỉ có nghiệm duy nhất với mọi m. Hay không tồn tại giá trị của m để pt có 3 nghiệm phân biệt
3. Tìm m để pt: [TEX]x^3-3x^2+1-m=0[/TEX](1) có 3 nghiệm phân biệt thỏa mãn: [TEX]x_1<1<x_2<x_3[/TEX]
Với câu hỏi có chút biến đổi như vậy thì ta vẫn chỉ cần cô lập và lập BBT là được:
[TEX]m=x^3-3x^2+1[/TEX]
Lập BBT của [TEX]f(x)=x^3-3x^2+1[/TEX] ta được sự biến thiên của f(x) như sau:
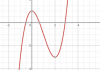
Ta có f(1)=-1 , vẽ đường y = -1 ta có:
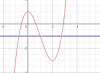
Ta thấy nếu [TEX]m \geq -1[/TEX] thì đường nằm ngang y=m sẽ cao hơn đường màu tím, như vậy dễ thấy hoành độ cắt tại 2 điểm [TEX]x_1,x_2 \leq 1[/TEX] không thỏa mãn
Từ đây ta có điều kiện của m là: [TEX]-3<m<-1[/TEX] (m>-3 là điều kiện chặn dưới để pt đủ 3 nghiệm phân biệt )
1. Pt có nghiệm x=a cố định với mọi m, thì ta cố gắng phân tích f(x)=(x-a)g(x) với g(x) là đa thức bậc 2, từ đó dùng delta để biện luận số nghiệm thỏa mãn
2. PT không có các nghiệm cố định, ta cố gắng cô lập m và x. Từ đó đưa về PT g(x)=m. Khảo sát vẽ BBT của g(x), số nghiệm pt g(x)=m chính bằng số giao điểm đường thẳng nằm ngang y=m và g(x)
Các bài toán phân tích được nhân tử đã được nêu ở đây , nên ở đây chỉ nêu về các bài toán cô lập.
1. Biện luận theo m để số nghiệm của phương trình [TEX]x^2-3x-m=0(1)[/TEX]
Lời giải: ta có [tex](1)<=>x^2-3x=m[/tex]
Khảo sát hàm [TEX]f(x)=x^3-3x[/TEX] , ta có [TEX]f'(x)=3x^2-3;f'(x)=0<=>x=-1;x=1[/TEX]
Từ đó ta lập được BBT và suy ra được dạng đồ thị của hàm f(x) như sau:
Từ đồ thị ta thấy, với m>2 hoặc m<-2 thì pt đã cho có nghiệm duy nhất
Với m=2 hoặc m=-2 thì pt đã cho có 2 nghiệm, trong đó có 1 nghiệm kép
Với -2<m<2 thì pt đã cho có 3 nghiệm phân biệt.
2. Tìm m để pt : [TEX]x^3+x^2(m+1)+3x+m=0[/TEX](1) có 3 nghiệm phân biệt.
Để cô lập được ta phải nhóm các số hạng có chứa m vào với nhau:
(1)<=>[tex]x^3+x^2+3x+m(x^2+1)=0<=>m=\frac{-(x^3+x^2+3x)}{x^2+1}[/tex]
Khảo sát hàm [TEX]f(x)=\frac{-(x^3+x^2+3x)}{x^2+1}[/TEX]
Ta có: [tex]f'(x)=-\frac{x^4+2x+3}{(x^2+1)^2}[/tex] , ta thấy [TEX]f'(x)<0[/TEX] với mọi x, do đó hàm f(x) NB trên R
Vậy ta có đồ thị f(x) như sau :
Vậy pt đã cho luôn chỉ có nghiệm duy nhất với mọi m. Hay không tồn tại giá trị của m để pt có 3 nghiệm phân biệt
3. Tìm m để pt: [TEX]x^3-3x^2+1-m=0[/TEX](1) có 3 nghiệm phân biệt thỏa mãn: [TEX]x_1<1<x_2<x_3[/TEX]
Với câu hỏi có chút biến đổi như vậy thì ta vẫn chỉ cần cô lập và lập BBT là được:
[TEX]m=x^3-3x^2+1[/TEX]
Lập BBT của [TEX]f(x)=x^3-3x^2+1[/TEX] ta được sự biến thiên của f(x) như sau:
Ta có f(1)=-1 , vẽ đường y = -1 ta có:
Ta thấy nếu [TEX]m \geq -1[/TEX] thì đường nằm ngang y=m sẽ cao hơn đường màu tím, như vậy dễ thấy hoành độ cắt tại 2 điểm [TEX]x_1,x_2 \leq 1[/TEX] không thỏa mãn
Từ đây ta có điều kiện của m là: [TEX]-3<m<-1[/TEX] (m>-3 là điều kiện chặn dưới để pt đủ 3 nghiệm phân biệt )
