S
son_9f_ltv
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Tác giả: ngoduykhanh đưa lên lúc: 21:03:25 Ngày 01-02-2008
bất đẳng thức Bernoulli là một bất đẳng thức cho phép tính gần đúng các lũy thừa của 1 + x.Bất đẳng thức này được phát biểu như sau:

<IMG class=tex alt="(1 + x)^r > 1 + rx\!" src="http://upload.wikimedia.org/math/a/2/4/a248be9dec5f64c2cbdcb2f04ae14ac3.png"> với mọi số nguyên r ≥ 2 và với mọi số thực x ≥ −1 với x ≠ 0.
Bất đẳng thức Bernoulli thường được dùng trong việc chứng minh các bất đẳng thức khác. Bản thân nó có thể được chứng minh bằng phương pháp quy nạp toán học:
Chứng minh:
Khi r=0, bất đẳng thức trở thành


Bây giờ giả sử bất đẳng thức đúng với r=k:

Cần chứng minh:

Thật vậy,
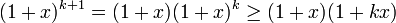



=> Bất đẳng thức đúng với r=k+1.
Theo nguyên lý quy nạp, chúng ta suy ra bất đẳng thức đúng với mọi
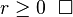
Số mũ r có thể tổng quát hoá thành số thực bất kỳ như sau: nếu x > −1, thì


Có thể chứng minh bất đẳng thức tổng quát hoá nói trên bằng cách so sánh các đạo hàm.
Một lần nữa, bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt nếu x ≥ -1 và 1 ≤ r thuộc tập số tự nhiên.
Các bất đẳng thức liên quan Bất đẳng thức dưới đây ước lượng lũy thừa bậc r của 1 + x theo chiều khác. Với số thực x bất kỳ, r > 0, chúng ta có



Lưu ý tất cả các thành viên khi tham gia diễn đàn **********: Chỉ đưa lên diễn đàn các tài liệu do mình sở hữu hoặc được sự cho phép của chủ sở hữu. Các đơn vị phát hiện thấy nội dung do các thành viên đưa lên ********** là sở hữu của mình mà không được phép xin liên hệ với ban quản trị để chúng tôi kịp thời gỡ bỏ



mọi người chịu khó nha mình copy từ diễn đàn o********** về nên nó bị như vậy
mọi người chịu khó bôi đen mà đọc cho dễ nha

