C
conhoaitrongkyuc1208
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
[TEX]\blue \frac{\sum_{cyc}\(a+b\)\(a+c\)}{\prod_{cyc} \(a+b\)}\ge \frac{5}{2} \Leftrightarrow \frac{\sum_{cyc}(a^2+1\)}{a+b+c-abc}\ge \frac{5}{2} [/TEX]thỏa mãn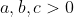 . Chứng minh :
. Chứng minh :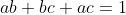

[TEX]\blue \Leftrightarrow 2\[\(a+b+c\)^2+1\]-5\(a+b+c\)+5abc\ge 0 [/TEX]
[TEX]\blue \Leftrightarrow 2\(a+b+c-2\)^2+3\(a+b+c\)+5abc-6\ge 0[/TEX]
giả sử [TEX]\blue a=max\{a,b,c\}[/TEX] lúc đó ta có :
[TEX]\blue \Leftrightarrow 2\(a+b+c-2\)^2+\frac{3\(b+c-1\)^2+bc\(2-5bc\)}{b+c}\ge 0[/TEX]
Mà nó thì luốn đúng do đó ta chứng minh xong
[TEX]A^2\sum_{cyc} a(a^2+kbc)\ge (a+b+c)^3[/TEX]Cho [TEX]a,b,c >0[/TEX] và [TEX]k\geq 8[/TEX]. Chứng minh rằng
[TEX]A:=\frac{a}{\sqrt{a^{2}+kbc}}+\frac{b}{\sqrt{b^{2}+kac}}+\frac{c}{\sqrt{c^{2}+kab}}\geq\frac{3}{ \sqrt{1+k} }[/TEX][TEX]k=8[/TEX] chính là đề IMO 42
Do đó chúng ta cần chứng minh.
[TEX](a+b+c)^3\ge \frac{9}{k+1} (a^3+b^3+c^3+3kabc) [/TEX]
[TEX]\leftrightarrow (k+1)[\sum_{cyc}a^3+\sum_{cyc}3ab(a+b)+6abc]\ge 9(\sum_{cyc}a^3+3kabc)[/TEX]
[TEX]\leftrightarrow (x+9) [\sum_{cyc}a^3+\sum_{cyc}3ab(a+b)+6abc]\ge 9\sum_{cyc}a^3+216abc+27xabc [/TEX] [TEX]x\ge 0[/TEX]
[TEX]\leftrightarrow x[\sum_{cyc}a^3+\sum_{cyc}3ab(a+b)-27abc]+9 [\sum_{cyc}3ab(a+b)+6abc-24abc]\ge 0[/TEX]
Chúng ta luôn có rằng 1 điều thật tửng là :[TEX]a,b,c\ge 0; \sum a=3. Min: \sum \sqrt{a+3}[/TEX])
)
[TEX]\red \frac{\(\sqrt{6}-\sqrt{3}\)\(a+b+c\)+9\sqrt{3}}{3}\le \sum_{cyc}^{a,b,c\ge 0\ \ a+b+c=3} \sqrt{a+3}\le \sqrt{3}\sqrt{a+b+c+9} [/TEX]
khanhsy said:Cho [TEX]a,b,c,d>0[/TEX] thoả mãn [TEX]abcd=1[/TEX] chứng minh rằng khi đó ta có :
[TEX]\ \ \ \ \ \sum_{cyclic} \sqrt{a^2+1} \le \sqrt{2}\(a+b+c+d\)[/TEX]
[TEX]f(x)=\sqrt{x^2+1}-\sqrt{2}x+\(\sqrt{2}-\frac{1}{\sqrt{2}}\)lnx[/TEX]hãy chú ý said:Trước tiên anh giả sử tồn tại con [TEX]a[/TEX] thoả mãn
[TEX]f(x)=\sqrt{x^2+1}-\sqrt{2}x+alnx[/TEX]
sau đó muốn tìm [TEX]a[/TEX] buộc nó vào [TEX]f'(1)=0[/TEX]
[TEX]f'(x):= \frac{x}{\sqrt{x^2+1}}-\sqrt{2}+\frac{a}{x}[/TEX]
Chúng ta cần có [TEX]f'(1):=0 \righ a=\sqrt{2}-\frac{1}{\sqrt{2}} [/TEX]
[TEX]f'(x):= \frac{\(x-1\)\(x-2x^2-1-2\sqrt{2}\sqrt{x^2+1} \)}{\(x\sqrt{2x^2+2}\)\(\sqrt{2}x^2+\sqrt{x^2+1}\)}[/TEX]
[TEX]f'(x):=0 \leftrightarrow x=1[/TEX]
Từ bảng biến thiên chúng ta có :
[TEX]\sqrt{x^2+1}-\sqrt{2}x+\(\sqrt{2}-\frac{1}{\sqrt{2}}\)lnx \le 0 [/TEX]
Với [TEX]x=a,b,c,d[/TEX] cộng vế theo vế ta được đpcm.
[TEX]\blue \(a+b+c+\frac{1}{2}\)\(bc+ca+ab+2abc\)\ge{16abc}[/TEX]Cho các số thực không âm [TEX] a,b,c[/TEX] thỏa mãn [TEX] ab+bc+ca=1-2abc[/TEX]. Chứng minh rằng khi đó ta có .
[TEX]\(a+b+c\)+1\ge 32abc[/TEX]
[TEX]\blue \[\frac{1}{\(1+a\)^2}+\frac{1}{\(1+b\)^2}-\frac{1}{1+ab}\]+\[\frac{1}{4}+\frac{1}{\(1+c\)^2}-\frac{1}{1+c}\]:=\frac{ab\(a-b\)^2+\(ab-1\)^2}{\(1+a\)^2\(1+b\)^2\(1+ab\)}+\frac{\(c-1\)^2}{4\(1+c\)^2}\ge 0[/TEX]khanhsy said:[TEX]\red a,b,c>0\ \ ,\ \ abc=1\ \ Cmr\ \ LHS:=\sum_{cyclic}\frac{1}{\(1+a\)^2}\ge \frac{3}{4}[/TEX]
[TEX]\red 3LHS-3:=\sum_{cyclic}\(\frac{3}{3-xy} -1\)=\sum_{cyclic}\frac{2xy}{\(x-y\)^2+\(z^2+x^2\)+\(z^2+y^2\)}[/TEX]khanhsy said:[TEX]a+b+c=3[/TEX], tìm max [TEX]\frac1{3-\sqrt{ab}} +\frac1{3-\sqrt{bc}} +\frac1{3-\sqrt{ca}}[/TEX]
[TEX]\ \ \le \sum_{cyclic}\frac{2xy}{\(z^2+x^2\)+\(z^2+y^2\)} \le \sum_{cyclic} \frac{\frac{x^2}{z^2+x^2}+\frac{y^2}{z^2+y^2}}{2}=\frac{3}{2}\righ LHS\le \frac{3}{2}[/TEX]
Rõ ràng bất đẳng thức có thể viết lại như sauCho[TEX] a,b,c >0[/TEX] và [TEX]a+b+c=3.[/TEX] Tìm min
[TEX]LHS:=\frac{a}{a+bc}+\frac{b}{b+ac}+\frac{c}{c+ab} \ge \frac{3}{2} [/TEX]
Nếu như các số thực dương [TEX]x,y,z[/TEX] thoả mãn [TEX]xy+yz+zx=3[/TEX] thì ta cần chứng minh
[TEX]LHS:=\sum_{cyclic} \frac{1}{1+x^2}\ge \frac{3}{2} [/TEX]
Thật vậy theo định lí chuồng bồ câu thì luôn tồn tại ít nhất một cặp số [TEX]\ge 1[/TEX]. Không mất tính tổng quát giả sử nó là [TEX]xy\ge 1[/TEX] suy ra
[TEX]\frac{1}{1+x^2}+\frac{1}{1+y^2}\ge \frac{2}{1+xy} [/TEX]
[TEX]\righ LHS\ge \frac{2}{1+xy}+\frac{1}{1+z^2} [/TEX]
Ta cần chứng minh
[TEX]\frac{2}{1+xy}+\frac{1}{1+z^2}\ge \frac{3}{2} [/TEX]
[TEX]\Leftrightarrow 2(3+2z^2+xy)\ge 3(1+z^2+xy+xyz^2)[/TEX]
[TEX]\Leftrightarrow z^2-xy+3\ge 3xyz^2[/TEX]
[TEX]\Leftrightarrow z^2+yz+zx\ge 3xyz^2[/TEX]
[TEX]\Leftrightarrow x+y+z\ge 3xyz[/TEX]
Bất đẳng thức cuối cùng luôn đúng do [TEX]Am-Gm[/TEX] vì
[TEX]x+y+z\ge 3\sqrt[3]{xyz}=(xy+yz+zx)\sqrt[3]{xyz}\ge 3xyz[/TEX]
Nếu như:
[TEX]\blue 3(1+r\)=p^2+pq+q^2[/TEX]
Ta luôn có:
[TEX]a^4+b^4+c^4+r\(a^2b^2+b^2c^2+c^2a^2\)+\(p+q-r-1\)abc\(a+b+c\) \ge p\(a^3b+b^3c+c^3a\)+q\(ab^3+bc^3+ca^3\)[/TEX]
Nó là luôn đúng vì :
[TEX]\blue LHS-RHS:=\sum_{cyclic} \[ 2a^2-b^2-c^2-pab+\(p+q\)bc-qca\]^2\ge 0[/TEX]
Last edited by a moderator:

