Toán 12 Bán kính mặt cầu.

[Zo_yaaaa]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cảm ơn các bạn đã quan tâm

 

[vangiang124]

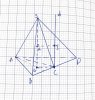
Gọi G là trọng tâm [tex]\Delta ABC[/tex] thì [tex]SG \perp (ABC)[/tex]
[TEX]CB=CA=CD[/TEX] nên C là tâm đường tròn ngoại tiếp [TEX]\Delta ABD[/TEX]
Gọi [TEX]I\in d[/TEX] là tâm mặt cầu cần tìm
[TEX]IC=x[/TEX] [TEX]\rightarrow[/TEX] [TEX]SK=|SG-x|[/TEX]
[TEX]IK\perp SG[/TEX]
[TEX]\rightarrow[/TEX] [TEX]IK=CG=AG=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}[/TEX]
[TEX]SG=\sqrt{SA^2-AG^2} = a[/TEX]
[TEX]IS=ID \leftrightarrow IK^2 +SK^2=IC^2 +CD^2[/TEX]
[TEX]\leftrightarrow \frac{a^2}{3} +(a-x)^2 =x^2 +a^2 [/TEX]
[TEX]\rightarrow x=\frac{a}{6}[/TEX]
Vậy bán kính mặt cầu cần tìm là
[TEX]R=\sqrt{x^2+a^2} =\frac{a\sqrt{37}}{6}[/TEX]

XEM TRƯỚC