 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
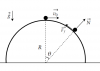
Đề: Một viên bi nhỏ khối lượng m trượt trên mặt bán cầu nhẵn, bán kính R, được giữ cố định. Hạt xuất phát từ đỉnh quả cầu với vận tốc ban đầu [TEX]\vec {v_0}[/TEX] nằm ngang. Hệ số ma sát giữa viên bi và bán cầu là [TEX]\mu[/TEX]
a,b, Xét trường hợp [TEX]0<\mu \leq 1[/TEX]. Chứng tỏ rằng vận tốc của hạt khi nó đang trượt trên bán cầu tại vị trí [TEX]\theta[/TEX] được cho bởi hệ thức:
[TEX]v(\theta) = \sqrt{Rg}[\frac{2(2\mu^2\cos\theta-3\mu\sin\theta-\cos\theta)}{1+4\mu^2}+(\frac{v_0^2}{Rg}+\frac{2-4\mu^2}{1+4\mu^2})e^{2\mu\theta}]^{1/2}[/TEX]
mong các bác giúp, bài từ số 217 vật lý tuổi trẻ, nhưng e ko có số 218 . biểu thức thế kia chắc chắn là p đi tìm [TEX]s(\theta)[/TEX] rồi, cơ mà e ko biết làm ra sao.
. biểu thức thế kia chắc chắn là p đi tìm [TEX]s(\theta)[/TEX] rồi, cơ mà e ko biết làm ra sao.
a,b, Xét trường hợp [TEX]0<\mu \leq 1[/TEX]. Chứng tỏ rằng vận tốc của hạt khi nó đang trượt trên bán cầu tại vị trí [TEX]\theta[/TEX] được cho bởi hệ thức:
[TEX]v(\theta) = \sqrt{Rg}[\frac{2(2\mu^2\cos\theta-3\mu\sin\theta-\cos\theta)}{1+4\mu^2}+(\frac{v_0^2}{Rg}+\frac{2-4\mu^2}{1+4\mu^2})e^{2\mu\theta}]^{1/2}[/TEX]

mong các bác giúp, bài từ số 217 vật lý tuổi trẻ, nhưng e ko có số 218
Last edited:

