- 18 Tháng hai 2020
- 71
- 97
- 71
- 19
- Hà Nội
- Trường quân đội liệt hỏa
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
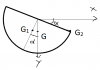
Người ta đặt mặt lồi của bán cầu trên một mặt phẳng nằm ngang tại mép của bán cầu đặt một vật nhỏ làm cho mặt phẳng bán cầu nghiêng đi một góc alpha so với mặt nằm ngang biết khối lượng bán cầu là m1,của vật nhỏ là m2. trọng tâm G của bán cầu cách tâm hình học của mặt cầu là 3R/8 trong đó R là bán kính của bán cầu Tính góc alpha