Bài toán trung điểm của đoạn thẳng

[huongbloom]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

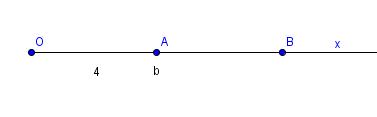
Bài 1: Cho A,B thuộc tia Ox sao cho OA=4cm, OB=b (b>4). Tìm điều kiện của b để a là trung điểm của OB
Bài 2: Cho AB=6cm. Lấy E trên đường thẳng AB sao cho AE= $\frac{2}{3}$ AB. Gọi F là trung điểm của AE.
a) Có phải E là trung điểm của BF hay không?
b) Gọi O là trung điểm của EF. Khi nào thì O cũng là trung điểm của AB?
Bài 3: Cho đoạn thẳng $AA^{\circ}$ = 1 đơn vị.
a) Lấy $A^{1}$ là trung điểm của $AA^{\circ}$. Tính tỉ số $\frac{AA^{\circ}}{AA^{1}}$
b) Tương tự lấy $A^{2}$, $A^{3}$ ... $A^{10}$ lần lượt là các trung điểm của các đoạn thẳng $AA^{1}$, $AA^{2}$ ... $AA^{9}$.
Hãy so sánh $\frac{AA^{\circ}}{AA^{1}}$+$\frac{AA^{\circ}}{AA^{2}}$+...+$\frac{AA^{\circ}}{AA^{10}}$ với $2^{11}$

 

[chaugiang81]

bài 2.


ta có :
AE= 6/3*2 = 4cm. => EB = 2cm
F là trung điểm AE nên AF= FE= 2cm= EB
FB = 2 +2 = 4cm.
mà FE= EB(=2cm) nên E là trung điểm của AB.
vì O là trung điểm của FE nên OF = OE = 1cm
=> OF + AF= OE + EB
<=> AO =OB( 3=3)
hay O đã là trung điểm của AB. vậy O là trung điểm của AB khi O cách đều hai đầu mút A,B của đoạn thẳng

 

[iceghost]

Bài 1

Đề sai, b > 4 thì đúng hơn

Khi A là trung điểm OB
\Rightarrow $\frac12 OB = \frac12b = OA = 4$
\Rightarrow $b = 2.4=8$

Vậy khi b = 8 thì A là trung điểm OB

 

[linhchi254]

Bài 2:
AE=2/3.6=4(cm)
\Rightarrow EB=2(cm)
F là trung điểm của AE\Rightarrow FE=2(cm)
FE=EB\Rightarrow E là trung điểm của FB
O là trung điểm của FE\RightarrowFO=OE=1(cm)
\Rightarrow AF+FO=OE+EB
\Rightarrow OA=OB\Leftrightarrow O là trung điểm của AB
O là trung điểm của AB khi O cách đều 2 đầu mút A và B của đoạn thẳng