 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
cho đường tròn tâm O bán kính R và dây AB . vẽ đường kính CD vuông góc với AB tại E ( D thuộc cung nhỏ AB) . M là điểm thuộc cung nhỏ BC .Gọi F là giao điểm DM và AB . Tia CM cắt đường thẳng AB tại K. Tiếp tuyến tại M của đường tròn (O) cắt AF tại T. Chứng minh rằng FB /KB = EF/ EA
em tìm theo kiểu tách nó ra rồi chứng minh FB/ KA + FB/EA =1
nhưng không biết làm thế nào nữa
những phần trước đã chứng minh là tứ giác CEFMlaf tứ giác nội tiếp, AD^2= DF.DM/ và IK=IF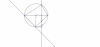
em tìm theo kiểu tách nó ra rồi chứng minh FB/ KA + FB/EA =1
nhưng không biết làm thế nào nữa
những phần trước đã chứng minh là tứ giác CEFMlaf tứ giác nội tiếp, AD^2= DF.DM/ và IK=IF


