- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I. tiếp tuyến của một đường cong (C) tại 1 điểm thuộc (C)
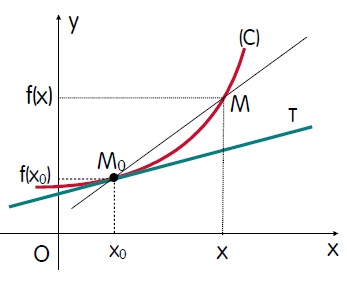
- cho hàm số [tex]y=f(x)[/tex] có đồ thị là đường cong (C). điểm [tex]M(x_0;y_0)[/tex] thuộc đồ thị (C). khi đó, tiếp tuyến của đồ thị (C) tại điểm M là:
[tex]y=f'(x_0).(x-x_0)+y_0[/tex]
- với [tex]k=f'(x_0)[/tex] là hệ số góc của tiếp tuyến. từ đó, nhiều bài toán liên quan đến hệ số góc k.
- nếu A, B thuộc đồ thị (C). khi đó: [tex]K_A=f'(x_A);k_B=f'(x_B)[/tex]
+ nếu [tex]k_A=k_B[/tex] thì tiếp tuyến tại A và B song song hoặc trùng nhau.
+ nếu [tex]k_A.k_B=-1[/tex] thì 2 tiếp tuyến tại A và B vuông góc.
+ góc giữa 2 đường thẳng: [tex]tan\alpha =\left | \frac{k_A-k_B}{1+k_A.k_B} \right |[/tex]
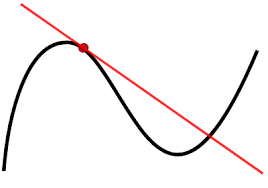
- chú ý: tiếp tuyến tại 1 điểm có thể cắt đồ thị hàm số
- ví dụ 1: hàm số [tex]y=\frac{1}{3}x^3-\frac{1}{2}x^2+x+1[/tex] có đồ thị (C). tìm tiếp tuyến của (C) có hệ số góc nhỏ nhất.
- ta có hệ số góc của tiếp tuyến của (C): [tex]k=y'=x^2-x+1=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}[/tex]
vậy, hệ số góc nhỏ nhất của tiếp tuyến là [tex]k=\frac{3}{4}[/tex] tại [tex]M(\frac{1}{2};\frac{17}{12})[/tex].
vậy, tiếp tuyến có phương trình: [tex]y=\frac{3}{4}(x-\frac{1}{2})+\frac{17}{12}[/tex]
II. tiếp tuyến đi qua 1 điểm nằm ngoài đồ thị - sự tiếp xúc của 2 đường cong
- hàm số [tex]y=f(x)[/tex] có đồ thị là (C). điểm [tex]A(x_0;y_0)[/tex] là điểm nằm ngoài đồ thị hàm số. viết phương trình tiếp tuyến của (C) đi qua A.
+ giả sử tiếp tuyến có hệ số góc là k, khi đó ta có phương trình tiếp tuyến của (C) đi qua A: [tex]y=k(x-x_0)+y_0[/tex]
+ để đường thẳng trên là tiếp tuyến của (C) thì hệ sau phải có nghiệm:
[tex]\left\{\begin{matrix} f(x)=y\\ f'(x)=y' \end{matrix}\right. <=>\left\{\begin{matrix} f(x)=k(x-x_0)+y_0\\ f'(x)=k \end{matrix}\right.[/tex]
- mở rộng ra cho 2 đường cong: 2 đường cong tiếp xúc với nhau tại 1 điểm nếu 2 đường cong có chung 1 tiếp tuyến tại điểm đó.
- điều kiện để 2 đường cong tiếp xúc nhau: hàm số f(x) có đồ thị [tex](C_1)[/tex], hàm số g(x) có đồ thị [tex](C_2)[/tex]. hai đồ thị tiến xúc nhau nếu hệ sau có nghiệm:
[tex]\left\{\begin{matrix} f(x)=g(x)\\ f'(x)=g'(x) \end{matrix}\right.[/tex]
- ví dụ 1: cho hàm số [tex]y=\frac{-x+2}{x-1}[/tex] có đồ thị (C) và điểm A(a;1). tìm a để có đúng 1 tiếp tuyến của (C) đi qua A. ( đề minh họa toán THPTQG 2018)
+ gọi đường thẳng đi qua A và tiếp xúc với đồ thị (C) có phương trình là [tex]y=k(x-a)+1[/tex]. điều kiện tiếp xúc: [tex]\left\{\begin{matrix} \frac{-x+2}{x-1}=k(x-a)+1\\ \frac{-1}{(x-1)^2}=k \end{matrix}\right. =>\frac{-x+2}{x-1}=-\frac{x-a}{(x-1)^2}+1<=>2x^2-6x+3+a=0[/tex]
để chỉ có 1 tiếp tuyến qua A thì pt trên chỉ có 1 nghiệm kép:
=> [tex]\Delta =0<=>6^2-4.2.3.a=0<=>a=\frac{3}{2}[/tex]
hoặc có 2 nghiệm phân biệt với 1 nghiệm bằng 1:
[tex]\left\{\begin{matrix} 6^2-4.2.3.a>0\\ 2-6+3+a= 0 \end{matrix}\right. <=>\left\{\begin{matrix} a< \frac{3}{2}\\ a=1 \end{matrix}\right.<=>a=1[/tex]
vậy có 2 giá trị là [tex]a=\frac{3}{2};a=1[/tex]
@YuuDuong @thomnguyen1961
- cho hàm số [tex]y=f(x)[/tex] có đồ thị là đường cong (C). điểm [tex]M(x_0;y_0)[/tex] thuộc đồ thị (C). khi đó, tiếp tuyến của đồ thị (C) tại điểm M là:
[tex]y=f'(x_0).(x-x_0)+y_0[/tex]
- với [tex]k=f'(x_0)[/tex] là hệ số góc của tiếp tuyến. từ đó, nhiều bài toán liên quan đến hệ số góc k.
- nếu A, B thuộc đồ thị (C). khi đó: [tex]K_A=f'(x_A);k_B=f'(x_B)[/tex]
+ nếu [tex]k_A=k_B[/tex] thì tiếp tuyến tại A và B song song hoặc trùng nhau.
+ nếu [tex]k_A.k_B=-1[/tex] thì 2 tiếp tuyến tại A và B vuông góc.
+ góc giữa 2 đường thẳng: [tex]tan\alpha =\left | \frac{k_A-k_B}{1+k_A.k_B} \right |[/tex]
- chú ý: tiếp tuyến tại 1 điểm có thể cắt đồ thị hàm số
- ví dụ 1: hàm số [tex]y=\frac{1}{3}x^3-\frac{1}{2}x^2+x+1[/tex] có đồ thị (C). tìm tiếp tuyến của (C) có hệ số góc nhỏ nhất.
- ta có hệ số góc của tiếp tuyến của (C): [tex]k=y'=x^2-x+1=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}[/tex]
vậy, hệ số góc nhỏ nhất của tiếp tuyến là [tex]k=\frac{3}{4}[/tex] tại [tex]M(\frac{1}{2};\frac{17}{12})[/tex].
vậy, tiếp tuyến có phương trình: [tex]y=\frac{3}{4}(x-\frac{1}{2})+\frac{17}{12}[/tex]
II. tiếp tuyến đi qua 1 điểm nằm ngoài đồ thị - sự tiếp xúc của 2 đường cong
- hàm số [tex]y=f(x)[/tex] có đồ thị là (C). điểm [tex]A(x_0;y_0)[/tex] là điểm nằm ngoài đồ thị hàm số. viết phương trình tiếp tuyến của (C) đi qua A.
+ giả sử tiếp tuyến có hệ số góc là k, khi đó ta có phương trình tiếp tuyến của (C) đi qua A: [tex]y=k(x-x_0)+y_0[/tex]
+ để đường thẳng trên là tiếp tuyến của (C) thì hệ sau phải có nghiệm:
[tex]\left\{\begin{matrix} f(x)=y\\ f'(x)=y' \end{matrix}\right. <=>\left\{\begin{matrix} f(x)=k(x-x_0)+y_0\\ f'(x)=k \end{matrix}\right.[/tex]
- mở rộng ra cho 2 đường cong: 2 đường cong tiếp xúc với nhau tại 1 điểm nếu 2 đường cong có chung 1 tiếp tuyến tại điểm đó.
- điều kiện để 2 đường cong tiếp xúc nhau: hàm số f(x) có đồ thị [tex](C_1)[/tex], hàm số g(x) có đồ thị [tex](C_2)[/tex]. hai đồ thị tiến xúc nhau nếu hệ sau có nghiệm:
[tex]\left\{\begin{matrix} f(x)=g(x)\\ f'(x)=g'(x) \end{matrix}\right.[/tex]
- ví dụ 1: cho hàm số [tex]y=\frac{-x+2}{x-1}[/tex] có đồ thị (C) và điểm A(a;1). tìm a để có đúng 1 tiếp tuyến của (C) đi qua A. ( đề minh họa toán THPTQG 2018)
+ gọi đường thẳng đi qua A và tiếp xúc với đồ thị (C) có phương trình là [tex]y=k(x-a)+1[/tex]. điều kiện tiếp xúc: [tex]\left\{\begin{matrix} \frac{-x+2}{x-1}=k(x-a)+1\\ \frac{-1}{(x-1)^2}=k \end{matrix}\right. =>\frac{-x+2}{x-1}=-\frac{x-a}{(x-1)^2}+1<=>2x^2-6x+3+a=0[/tex]
để chỉ có 1 tiếp tuyến qua A thì pt trên chỉ có 1 nghiệm kép:
=> [tex]\Delta =0<=>6^2-4.2.3.a=0<=>a=\frac{3}{2}[/tex]
hoặc có 2 nghiệm phân biệt với 1 nghiệm bằng 1:
[tex]\left\{\begin{matrix} 6^2-4.2.3.a>0\\ 2-6+3+a= 0 \end{matrix}\right. <=>\left\{\begin{matrix} a< \frac{3}{2}\\ a=1 \end{matrix}\right.<=>a=1[/tex]
vậy có 2 giá trị là [tex]a=\frac{3}{2};a=1[/tex]
@YuuDuong @thomnguyen1961
