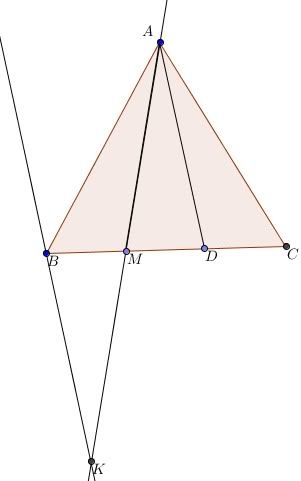
Lấy D thuộc MC sao cho [TEX]BM=MD=DC[/TEX]. Dễ chứng minh được [TEX]AM=AD[/TEX] (bằng cách chứng minh [TEX]\bigtriangle AMB= \bigtriangle ADC[/TEX] (c.g.c))
Trên tia đối tia AM lấy điểm K sao cho [TEX]AM=KM[/TEX].
Khi đó [TEX]\bigtriangle MBK= \bigtriangle MDA[/TEX] (c.g.c)
Dẫn đến [TEX]AD=BK[/TEX].
Ta có tam giác AMD cân ở A nên góc M và góc D nhọn. Do đó góc AMB tù.
Trong tam giác AMB có góc AMB tù nên [TEX]AB>AM \Rightarrow AB>AD \Rightarrow AB>BK[/TEX].
Trong tam giác ABK thì góc AB>BK nên [TEX]\widehat{K}= \widehat{BAM}[/TEX].
Mà [TEX]\widehat{K}=\widehat{MAD}[/TEX] (do [TEX]\bigtriangle MBK= \bigtriangle MDA[/TEX]) nên [TEX]\widehat{MAD}>\widehat{BAM[/TEX].
Do [TEX]\widehat{MAB}=\widehat{DAC}[/TEX] (do [TEX]\bigtriangle AMB= \bigtriangle ADC[/TEX]).
Khi đó mà [TEX]\widehat{BAM}+ \widehat{MAD}+ \widehat{ADC}=60^o[/TEX]
[TEX]\Rightarrow 2. \widehat{BAM}+ \widehat{MAD}=60^o[/TEX]
[TEX]\Rightarrow 3. \widehat{BAM} <60^o[/TEX]
[TEX]\Rightarrow \widehat{BAM}<20^o[/TEX].
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
