Vật lí 10 Bài toán ròng rọc động

[tibapro1234@gmail.com]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

cho em hỏi làm sao mình biến đổi ra như thế này ạ? em cảm ơn

 

[Vie Hoàng]

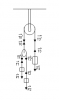
Dùng phép chiếu ta có:
[tex]P1-T1=m1a1=m1(a1'+a0) (1)[/tex]
[tex]P2-T2=m2a2=m2(a2'+a0) (2)[/tex]
[tex]P3-T3=m3a3=m3a0 (3)[/tex]
Lấy [tex](1)-(2)[/tex] ta được [tex]P1-P2=m1(a1'+a0)-m2(a2'+a0)[/tex]
[tex]<=>g(m1-m2)=a0.(m1-m2)+a1'(m1+m2)(4) (do a1'=-a2')[/tex]
Lấy [tex](1)-\frac{(3)}{2}[/tex] ta được [tex] \frac{P3}{2}-T1-P1+T1=g(\frac{m3}{2}-m1)=\frac{m3a0}{2}-m1(a1'+a0) (do T3=2T1=2T2)[/tex]
[tex]<=> g(\frac{m3}{2}-m1)=a0(\frac{m3}{2}-m1)-m1a1'[/tex]
[tex]\begin{matrix} <=>(a0-g)(\frac{m3}{2}-m1)=a1'm1\\ <=>(a0-g)(\frac{m3}{2m1}-1)=a1'(5)\end{matrix}[/tex]
Thay (5) vào (4), giải ra sẽ được.