Toán 9 Bài Toán Hình 9 nè :3. Đăng lại

[Quangtrannb68]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

P/S: Câu a) lm đk òi nha

 

[Kar Kar]

Câu b dùng đồng dạng.câu c nghĩ chưa ra

 

[Ann Lee]

View attachment 53692
P/S: Câu a) lm đk òi nha

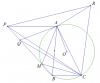
Câu b:
Vì AP=AB( câu a) [tex]\Rightarrow \Delta APB[/tex] cân tại A [tex]\Rightarrow \widehat{APB}=\widehat{ABQ}[/tex]
Lại có [tex]\widehat{QAM}=\widehat{ABM}[/tex] ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AM của (O) )
[tex]\Rightarrow \widehat{APM}=\widehat{MAQ}[/tex]
[tex]\Delta MAQ\sim \Delta \Delta MPA(g-g)[/tex]
[tex]\Rightarrow \frac{MA}{MP}=\frac{MQ}{MA}\Rightarrow MA^{2}=MP.MQ[/tex] (đpcm)
Câu c:
Có $\widehat{PAR}=360^{\circ}-\widehat{PAC}-\widehat{RAC}$
$=180^{\circ}+\widehat{ACB}-\widehat{CAQ}$
$=180^{\circ}+\widehat{ACB}-(\widehat{CAM}+\widehat{MAQ})$
$=\widehat{ACB}+\widehat{MBC}-\widehat{MBA}$
$=\widehat{ACB}+\widehat{ABC}$
$=180^{\circ}-\widehat{BAC}$
$=\widehat{PMC}$
Vì Q đối xứng R qua AC nên AQ=AR
Có: [tex]\frac{AP}{AR}=\frac{AP}{AQ}=\frac{MP}{MA}=\frac{MP}{MC}[/tex]
[tex]\Rightarrow \Delta PAR\sim \Delta PMC(c-g-c)\Rightarrow \widehat{APR}=\widehat{CPB}[/tex]
Nguồn: Đáp án đề thi thử vào 10 môn Toán chuyên KHTN năm 2018 vòng 1- đợt 1

 

[thuannguyen0803@gmail.com]

Tai sao AP = AB vay cac ban?????? Minh ngu toan hinh lam

 

[Quangtrannb68]

Câu b dùng đồng dạng.câu c nghĩ chưa ra

Bn sống ở đâu thế???