- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
I. Lý thuyết
1. hàm đa thức bậc 3: [tex]y=ax^3+bx^2+cx+d[/tex]
[tex]y'=3ax^2+2bx+c[/tex]
hàm số có 2 điểm cực trị khi và chỉ khi [tex]y'=0[/tex] có 2 nghiệm phân biệt [tex]x_1[/tex] và [tex]x_2[/tex].
[tex]\left\{\begin{matrix} a\neq 0\\ b^2-3ac> 0 \end{matrix}\right.[/tex]
- hệ thức vi-et: [tex]\left\{\begin{matrix} x_1+x_2=\frac{-2b}{3a}\\ x_1.x_2=\frac{c}{3a} \end{matrix}\right.[/tex]
đồ thị hàm số có dạng như sau:
+ hệ số a>0:
+ hệ số a<0:
.png)
2. hàm trùng phương: [tex]y=ax^4+bx^2+c[/tex]
[tex]y'=4ax^3+2bx[/tex]
hàm số có 3 điểm cực trị khi và chỉ khi [tex]y'=0[/tex] có 3 nghiệm phân biệt [tex]x_1,x_2,x_3[/tex]
[tex]y'=0<=>4ax^3+2bx=0<=>x=0,x=\sqrt{\frac{-b}{2a}}[/tex]
như vậy, hàm số có 3 điểm cực trị khi [tex]a.b<0[/tex]
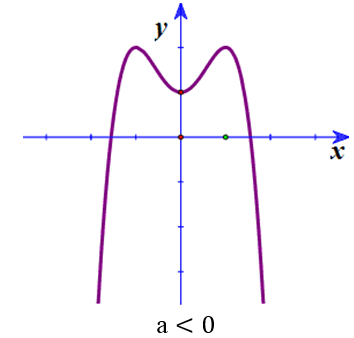
đồ thị hàm trùng phương có dạng:
+ hệ số a>0:
hệ số a<0:
3. hàm phân thức bậc 2 chia bậc nhất: [tex]y=\frac{ax^2+bx+c}{mx+n}[/tex]
[tex]y'=\frac{amx^2+2anx+bn-cm}{(mx+n)^2}[/tex]
hàm số có 2 điểm cực trị khi và chỉ khi [tex]y'=0[/tex] có 2 nghiệm phân biệt [tex]x_1[/tex] và [tex]x_2[/tex]
[tex]\left\{\begin{matrix} a\neq 0\\ \Delta > 0\\ x_1,x_2\neq \frac{-n}{m} \end{matrix}\right.[/tex]
II. ví dụ
ví dụ 1: cho hàm số [tex]y=2x^3+9mx^2+12m^2x+1[/tex]. tìm m để hàm số có 2 điểm cực trị, [tex]x_1[/tex] là điểm cực đại và [tex]x_2[/tex] là điểm cực tiểu sao cho [tex]x_1^2=x_2[/tex]
giải:
ta có: [tex]y'=6x^2+18mx+12m[/tex]
[tex]y'=0<=>6x^2+18mx+12m=0<=>x^2+3mx+2=0<=>(x+m)(x+2m)=0<=>x=-m,x=-2m[/tex]
để hàm số có 2 điểm cực trị thì [tex]m\neq 0[/tex]
xét với m<0, suy ra [tex]-m<-2m[/tex], do đó [tex]-m[/tex] là điểm cực đại, ta có:
[tex](-m)^2=-2m<=>m^2+2m=0<=>x=-2,m=0[/tex] (loại m=0)
xết với m>0, suy ra [tex]-m>-2m[/tex], do đó [tex]-2m[/tex] là điểm cực đại, ta có:
[tex](-2m)^2=-m<=>4m^2+m=0<=>m=0,m=\frac{-1}{2}[/tex] (loại cả 2)
do đó, m=-2 là giá trị duy nhất thỏa mãn.
ví dụ 2: tìm m để hàm số [tex]y=\frac{2}{3}x^3-mx^2-2(3m^2-1)x+\frac{2}{3}[/tex] có 2 điểm cực trị [tex]x_1, x_2[/tex] thỏa mãn [tex]x_1.x_2+2(x_1+x_2)=1[/tex]
giải:
ta có: [tex]y'=2x^2-2mx-2(3m^2-1)[/tex]
[tex]y'=0[/tex] có 2 nghiệm phân biệt khi [tex]\Delta > 0<=>m^2+4.(3m^2-1)>0<=>13m^2>4[/tex]
theo hệ thức vi-et, ta có: [tex]\left\{\begin{matrix} x_1+x_2=m\\ x_1.x_2=1-3m^2 \end{matrix}\right.[/tex]
thay vào điều kiện ban đầu, ta có:
[tex]1-3m^2+2m=1<=>m=0,m=\frac{2}{3}[/tex] (loại m=0)
do đó, giá trị duy nhất của m thỏa mãn là [tex]\frac{2}{3}[/tex]
1. hàm đa thức bậc 3: [tex]y=ax^3+bx^2+cx+d[/tex]
[tex]y'=3ax^2+2bx+c[/tex]
hàm số có 2 điểm cực trị khi và chỉ khi [tex]y'=0[/tex] có 2 nghiệm phân biệt [tex]x_1[/tex] và [tex]x_2[/tex].
[tex]\left\{\begin{matrix} a\neq 0\\ b^2-3ac> 0 \end{matrix}\right.[/tex]
- hệ thức vi-et: [tex]\left\{\begin{matrix} x_1+x_2=\frac{-2b}{3a}\\ x_1.x_2=\frac{c}{3a} \end{matrix}\right.[/tex]
đồ thị hàm số có dạng như sau:
+ hệ số a>0:
+ hệ số a<0:
2. hàm trùng phương: [tex]y=ax^4+bx^2+c[/tex]
[tex]y'=4ax^3+2bx[/tex]
hàm số có 3 điểm cực trị khi và chỉ khi [tex]y'=0[/tex] có 3 nghiệm phân biệt [tex]x_1,x_2,x_3[/tex]
[tex]y'=0<=>4ax^3+2bx=0<=>x=0,x=\sqrt{\frac{-b}{2a}}[/tex]
như vậy, hàm số có 3 điểm cực trị khi [tex]a.b<0[/tex]
đồ thị hàm trùng phương có dạng:
+ hệ số a>0:
hệ số a<0:
3. hàm phân thức bậc 2 chia bậc nhất: [tex]y=\frac{ax^2+bx+c}{mx+n}[/tex]
[tex]y'=\frac{amx^2+2anx+bn-cm}{(mx+n)^2}[/tex]
hàm số có 2 điểm cực trị khi và chỉ khi [tex]y'=0[/tex] có 2 nghiệm phân biệt [tex]x_1[/tex] và [tex]x_2[/tex]
[tex]\left\{\begin{matrix} a\neq 0\\ \Delta > 0\\ x_1,x_2\neq \frac{-n}{m} \end{matrix}\right.[/tex]
II. ví dụ
ví dụ 1: cho hàm số [tex]y=2x^3+9mx^2+12m^2x+1[/tex]. tìm m để hàm số có 2 điểm cực trị, [tex]x_1[/tex] là điểm cực đại và [tex]x_2[/tex] là điểm cực tiểu sao cho [tex]x_1^2=x_2[/tex]
giải:
ta có: [tex]y'=6x^2+18mx+12m[/tex]
[tex]y'=0<=>6x^2+18mx+12m=0<=>x^2+3mx+2=0<=>(x+m)(x+2m)=0<=>x=-m,x=-2m[/tex]
để hàm số có 2 điểm cực trị thì [tex]m\neq 0[/tex]
xét với m<0, suy ra [tex]-m<-2m[/tex], do đó [tex]-m[/tex] là điểm cực đại, ta có:
[tex](-m)^2=-2m<=>m^2+2m=0<=>x=-2,m=0[/tex] (loại m=0)
xết với m>0, suy ra [tex]-m>-2m[/tex], do đó [tex]-2m[/tex] là điểm cực đại, ta có:
[tex](-2m)^2=-m<=>4m^2+m=0<=>m=0,m=\frac{-1}{2}[/tex] (loại cả 2)
do đó, m=-2 là giá trị duy nhất thỏa mãn.
ví dụ 2: tìm m để hàm số [tex]y=\frac{2}{3}x^3-mx^2-2(3m^2-1)x+\frac{2}{3}[/tex] có 2 điểm cực trị [tex]x_1, x_2[/tex] thỏa mãn [tex]x_1.x_2+2(x_1+x_2)=1[/tex]
giải:
ta có: [tex]y'=2x^2-2mx-2(3m^2-1)[/tex]
[tex]y'=0[/tex] có 2 nghiệm phân biệt khi [tex]\Delta > 0<=>m^2+4.(3m^2-1)>0<=>13m^2>4[/tex]
theo hệ thức vi-et, ta có: [tex]\left\{\begin{matrix} x_1+x_2=m\\ x_1.x_2=1-3m^2 \end{matrix}\right.[/tex]
thay vào điều kiện ban đầu, ta có:
[tex]1-3m^2+2m=1<=>m=0,m=\frac{2}{3}[/tex] (loại m=0)
do đó, giá trị duy nhất của m thỏa mãn là [tex]\frac{2}{3}[/tex]
