[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
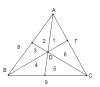
1. Cho tứ giác ABCD, E là giao điểm của các đường thẳng AB và CD, F là giao điểm của các đường thẳng BC và AD. Các tia phân giác của các góc E và F cắt nhau ở I. Chứng minh rằng:
a) Nếu góc BAD = 130 độ, góc BCD = 50 độ thì IE vuông góc với IF
b) Góc EIF bằng nửa tổng của một trong hai cặp góc đối của tứ giác ABCD
2. Chứng minh rằng nếu M là giao điểm của các đường chéo trong tam giác ABCD thì MA + MB + MC + MD nhỏ hơn hoặc bằng chu vi nhưng lớn hơn nửa chu vi tứ giác
3. Cho năm điểm trên mặt phẳng trong đó không có ba điểm nào thẳng hàng. CMR bao giờ cũng có thể chọn ra được 4 điểm là đỉnh của một tứ giác lồi
a) Nếu góc BAD = 130 độ, góc BCD = 50 độ thì IE vuông góc với IF
b) Góc EIF bằng nửa tổng của một trong hai cặp góc đối của tứ giác ABCD
2. Chứng minh rằng nếu M là giao điểm của các đường chéo trong tam giác ABCD thì MA + MB + MC + MD nhỏ hơn hoặc bằng chu vi nhưng lớn hơn nửa chu vi tứ giác
3. Cho năm điểm trên mặt phẳng trong đó không có ba điểm nào thẳng hàng. CMR bao giờ cũng có thể chọn ra được 4 điểm là đỉnh của một tứ giác lồi
Last edited:
bạn nghĩ kĩ xem ^^
