[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
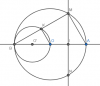
Cho đường tròn( O ) đường kính AB. Gọi I là trung điểm AO. Qua I ve dây cung MN vuông góc với AB. Ve đường tròn ( O' ) đường kính OB, đường tròn nay cắt MB tai K.
a/ Tính MA theo R
b/ CMR: N, O, K thẳng hàng
c/ CMR: IK la tiếp tuyến của đường tròn ( O')
Mong cac ban giup mik!!!!
Thanks nhiu

a/ Tính MA theo R
b/ CMR: N, O, K thẳng hàng
c/ CMR: IK la tiếp tuyến của đường tròn ( O')
Mong cac ban giup mik!!!!
Thanks nhiu