N
nhimcoi6
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho đoạn thẳng AB, Trên đoạn thẳng AB lấy 2 điểm M, N (M nằm giữa A và N). Vẽ về 1 phía của AB các tam giác đều AMD. MNE, NBF. gọi G là trọng tâm của tam giác DEF.
CMR: Khoảng cách từ G đến AB không phụ thuộc vào vị trí của M, N trên AB
@Toàn: Bài này hay !!
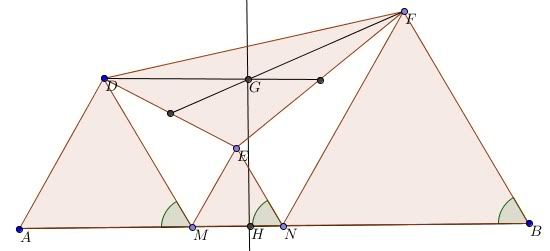
CMR: Khoảng cách từ G đến AB không phụ thuộc vào vị trí của M, N trên AB
@Toàn: Bài này hay !!

Last edited by a moderator:

