- 23 Tháng tám 2018
- 716
- 878
- 126
- Bình Định
- Trường THPT Số 1 An Nhơn
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
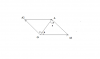
1.Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là x1 =A1 cos( omega t+0,35) ( cm) và x2=A2 cos( omega t-1,57) (cm). Dao động tổng hợp của hai dao động này có phương trình là x=A cos(omega t+ varphi ) (cm) . Gía trị cực đại (A1+A2) ?
2. Một vật thực hiện đồng thời hai dao động điều hòa theo phương trình dao động tổng hợp lần lượt là x1= 5cos ( omega t+ varphi )cm và x2= A2 cos (omega t- pi / 4) cm thì dao động tổng hợp là x=A cos( omega - pi /12 ) cm . Để biên độ A có giá trị bằng một nửa giá trị cực đại của chính nó thì biên độ A2 có giá trị?
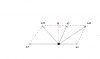
3. Cho D1, D2 ,D3 là ba dao động điều hòa cùng phương, cùng tần số. Dao động tổng hợp của D1, D2 có phương trình x12= 3 căn bậc hai 3 cos ( omega t + pi /2 ) cm . Dao động tổng hợp của D2 ,D3 có phương trình x23= 3cos ( omega t ) cm. Dao động D1 ngược pha với dao động D3. Biên độ dao động D2 có giá trị nhỏ nhất ?
4. Hai dao động điều hòa cùng phương , cùng tần số có phương trình x1 = A1 cos ( omega t- pi /6 ) cm và x2= A2 cos ( omega t + pi /2 ) cm. Dao động tổng hợp có phương trình x=căn bạc hai 3 cos ( omega t + varphi ) cm . Thay đổi giá trị của A1 để A2 có giá trị cực đại . Tìm giá trị A1 và \varphi khi đó.
2. Một vật thực hiện đồng thời hai dao động điều hòa theo phương trình dao động tổng hợp lần lượt là x1= 5cos ( omega t+ varphi )cm và x2= A2 cos (omega t- pi / 4) cm thì dao động tổng hợp là x=A cos( omega - pi /12 ) cm . Để biên độ A có giá trị bằng một nửa giá trị cực đại của chính nó thì biên độ A2 có giá trị?
3. Cho D1, D2 ,D3 là ba dao động điều hòa cùng phương, cùng tần số. Dao động tổng hợp của D1, D2 có phương trình x12= 3 căn bậc hai 3 cos ( omega t + pi /2 ) cm . Dao động tổng hợp của D2 ,D3 có phương trình x23= 3cos ( omega t ) cm. Dao động D1 ngược pha với dao động D3. Biên độ dao động D2 có giá trị nhỏ nhất ?
4. Hai dao động điều hòa cùng phương , cùng tần số có phương trình x1 = A1 cos ( omega t- pi /6 ) cm và x2= A2 cos ( omega t + pi /2 ) cm. Dao động tổng hợp có phương trình x=căn bạc hai 3 cos ( omega t + varphi ) cm . Thay đổi giá trị của A1 để A2 có giá trị cực đại . Tìm giá trị A1 và \varphi khi đó.
Last edited: