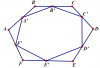
cho lục giác đều ABCDEF gọi A' , B' , C' , D' , E' ,F' lần lượt là trung điểm của các cạnh AB , BC , CD ,DE , EF ,FA . Cmr A' , B' , C' , D' , E' , F' là lục giác đều
______________________
Cái hình nó không đẹp lắm nha!
__
Lục giác đều sẽ có các cạnh bằng nhau: $AB=BC=CD=DE=EF=FA$
[tex]\Rightarrow A'B=BB'=B'C=CC'=C'D=DD'=D'E=EE'=E'F=FF'=F'A=AA'[/tex]
Và các góc của lục giác đều sẽ bằng: [tex]120^{\circ}[/tex]
Dễ dàng chứng minh được: [tex]\Delta BA'B'=\Delta CB'C'=\Delta DC'D'=\Delta ED'E'=\Delta FE'F'=\Delta AA'F'(c.g.c)[/tex]
[tex]\Rightarrow A'B'=B'C'=C'D'=D'E'=E'F'=F'A'[/tex]
Ta có: [tex]\widehat{BA'B'}=\frac{180^{\circ}-120^{\circ}}{2}=30^{\circ}[/tex]
Tương tự: [tex]\widehat{AA'F'}=30^{\circ}[/tex]
[tex]\Rightarrow \widehat{B'A'F'}=180^{\circ}-30^{\circ}-30^{\circ}=120[/tex] [tex]^{\circ}[/tex]
CMTT các góc còn lại bằng [tex]120^{\circ}[/tex]
Vậy [tex]A'B'C'D'E'F'[/tex] là lục giác đều
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.


