[Bài Tập] Kỹ thuật chọn điểm rơi trong bất đẳng thức Cauchy

[tthandb]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Bài 1. Cho

, chứng minh rằng

, với

. Nếu m = 1 là đề thi Đại học Khối D năm 2005.
Bài 2. Cho

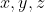là 3 số thỏa mãn

, chứng minh rằng:

(đề tham khảo 2005)
Bài 3. Cho

, tìm GTLN:

Bài 4. Cho

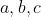là các số dương thỏa mãn

.
Chứng minh rằng:

(ĐTK 2005)
Bài 5. Cho

, tìm GTNN của các biểu thức sau:

Bài 6. Cho

, chứng minh rằng:

.
Bài 7. Cho a,b,c là các số dương. Tìm GTNN của:

(ĐHQGHN 2001-2002)
Bài 8. Cho a,b,c dương thỏa mãn abc = 1 , tìm GTNN của biểu thức:

(ĐH 2000 – 2001)
Bài 9. Cho

, tìm GTNN của

(ĐHNT 2001 – 2002)
Bài 10. Cho x,y,z là ba số dương và x + y + z \leq 1 , chứng minh rằng:

(ĐH 2003)
Bài 11: Cho a, b, c>0 thỏa mãn a + b+ c \leq 3/2 . Tìm Min của :

Bài 12: Cho a, b, c > 0 và a +2b +3c \geq 20. Tìm Min của

Mọi người cố gắng nhé, mình sẽ thanks nhiệt tình ​

 

[conga222222]

câu 1:
$\eqalign{
& do\;m \in N \to m \geqslant 1 \cr
& \to m + {x^3} + {y^3} \geqslant 1 + {x^3} + {y^3} \geqslant 3xy \cr
& \to \frac{{\sqrt {m + {x^3} + {y^3}} }}{{xy}} \geqslant \frac{{\sqrt 3 }}{{\sqrt {xy} }} \cr
& tuong\;tu... \cr
& \to VT \geqslant \frac{{\sqrt 3 }}{{\sqrt {xy} }} + \frac{{\sqrt 3 }}{{\sqrt {yz} }} + \frac{{\sqrt 3 }}{{\sqrt {zx} }} \geqslant 3\root 3 \of {\frac{{3\sqrt 3 }}{{\sqrt {{x^2}{y^2}{z^2}} }}} = 3\sqrt 3 \cr
& dau = \leftrightarrow m = x = y = z = 1 \cr} $

 

[tthandb]

câu 1:
$\eqalign{
& do\;m \in N \to m \geqslant 1 \cr
& \to m + {x^3} + {y^3} \geqslant 1 + {x^3} + {y^3} \geqslant 3xy \cr
& \to \frac{{\sqrt {m + {x^3} + {y^3}} }}{{xy}} \geqslant \frac{{\sqrt 3 }}{{\sqrt {xy} }} \cr
& tuong\;tu... \cr
& \to VT \geqslant \frac{{\sqrt 3 }}{{\sqrt {xy} }} + \frac{{\sqrt 3 }}{{\sqrt {yz} }} + \frac{{\sqrt 3 }}{{\sqrt {zx} }} \geqslant 3\root 3 \of {\frac{{3\sqrt 3 }}{{\sqrt {{x^2}{y^2}{z^2}} }}} = 3\sqrt 3 \cr
& dau = \leftrightarrow m = x = y = z = 1 \cr} $

Những bài còn lại bạn có giải được không? Chỉ cần nêu ra ý chính, không cần phải làm thật chi tiết

 

[tranvanhung7997]

Câu 8: $Q=\dfrac{bc}{a^2(b+c)}+\dfrac{ca}{b^2(c+a)}+\dfrac{ab}{c^2(a+b)}$
$=\dfrac{bc.abc}{a^2(b+c)}+\dfrac{ca.abc}{b^2(c+a)}+\dfrac{ab.abc}{c^2(a+b)}$
$=\dfrac{b^2c^2}{a(b+c)}+\dfrac{c^2a^2}{b(c+a)}+\dfrac{a^2b^2}{c(a+b)}$
Đặt $ab=x; bc=y; ca=z$ => xyz=1
=>$Q=\dfrac{y^2}{x+z}+\dfrac{z^2}{x+y}+\dfrac{x^2}{y+z}\ge\dfrac{(x+y+z)^2}{2(x+y+z)}=\dfrac{x+y+z}{2}$
$\ge \dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}$
Dấu = có <=>$ x=y=z=1$ <=> $a=b=c=1$

Bài 9: $P = \dfrac{x}{\sqrt[]{1 - x}} + \dfrac{y}{\sqrt[]{1 - y}} = \dfrac{x}{\sqrt[]{y}} + \dfrac{y}{\sqrt[]{x}}$
$= \dfrac{x^2}{x\sqrt[]{y}} + \dfrac{y^2}{y\sqrt[]{x}} \ge \dfrac{(x + y)^2}{ x\sqrt[]{y} + y\sqrt[]{x}}$ (Theo BĐT Cauchy - Schwazt)
= $\dfrac{1}{\sqrt[]{x} \sqrt[]{xy} + \sqrt[]{y}\sqrt[]{xy}} \ge \dfrac{1}{\sqrt[]{(x + y)(xy + xy)}}$ (Áp dụng BĐT Bunhiacopski ở mẫu)
=$\dfrac{1}{\sqrt[]{2xy}} \ge \dfrac{1}{\sqrt[]{2\dfrac{(x + y)^2}{4}}}$ (Áp dụng BĐT Cô Si ở mẫu)
= $\sqrt[]{2}$
Dấu = có <=> $x = y = \dfrac{1}{2}$

Cách làm tổng quát cho dạng bài 12 (có thể trong trường hợp 2 số, 3 số,.....)
$S = a + b + c + \dfrac{3}{a} + \dfrac{9}{2b} + \dfrac{4}{c}$
$= m(a + 2b + 3c) + (1 - m)a + \dfrac{3}{a} + (1 - m)b + \dfrac{9}{2b} + (1 - m)c + \dfrac{4}{c}$
Áp dụng BĐT Cô Si: $(1 - m)a +\dfrac{3}{a} \ge 2\sqrt[]{3(1 - m)}$
Dấu = có <=> $a = \sqrt[]{\dfrac{3}{1 - m}}$
$(1 - m)b + \dfrac{9}{2b} \ge 2\sqrt[]{9(1 - m)}$
Dấu = có <=> $b = \sqrt[]{\dfrac{9}{2(1 - m)}}$
$ (1 - m)c + \dfrac{4}{c} \ge 2\sqrt[]{4(1 - m)}$
Dấu = có <=> $c = \sqrt[]{\dfrac{4}{1 - m}}$
Cộng theo vế các BĐT trên ta được:
$S \ge 20m + 2\sqrt[]{3(1 - m)} + 2\sqrt[]{9(1 - m)} + 2\sqrt[]{4(1 - m)}$
Vậy ta chỉ cần tìm giá trị m thì bài toán sẽ được giải quyết. Việc tìm m là việc giải PT:
Ta thấy, dấu = có tại $a + 2b + 3c = 20$
<=> $$\sqrt[]{\dfrac{3}{1 - m}} + 2\sqrt[]{\dfrac{9}{2(1 - m)}} + 3\sqrt[]{\dfrac{4}{1 - m}} = 20$$
Trong bài này việc tìm m không khó vì chúng cùng mẫu nên dễ giải. Tuy nhiên ở các bài mà PT đó nhìn có vẻ khó giải thì ta chỉ cần nhập PT vào máy tính rồi nhẩm nghiệm thì ta được m (thường thì m có giá trị là số đẹp) vì cả phần trên chỉ là việc ngoài nháp, khi viết vào bài chỉ cần thay giá trị m vào là được.


Đó là cách mình nghĩ ra trong quá trình làm 1 số bài kiều như vậy. Nếu có gì đó sai sót thì các bạn góp ý thêm

 

[conga222222]

$\eqalign{
& bai\;4: \cr
& \cos i: \cr
& \left( {c + 3a} \right) + 1 + 1 \geqslant 3\root 3 \of {c + 3a} \cr
& \left( {a + 3b} \right) + 1 + 1 \geqslant 3\root 3 \of {a + 3b} \cr
& \left( {b + 3c} \right) + 1 + 1 \geqslant 3\root 3 \of {b + 3c} \cr
& \to 4\left( {a + b + c} \right) + 6 \geqslant 3\left( {\root 3 \of {a + 3b} + \root 3 \of {b + 3c} + \root 3 \of {c + 3a} } \right) \cr
& \leftrightarrow \root 3 \of {a + 3b} + \root 3 \of {b + 3c} + \root 3 \of {c + 3a} \leqslant \frac{{4\left( {a + b + c} \right) + 6}}{3} = 3 \cr
& dau = \leftrightarrow .... \cr} $

 

[tthandb]

Câu 8: $Q=\dfrac{bc}{a^2(b+c)}+\dfrac{ca}{b^2(c+a)}+\dfrac{ab}{c^2(a+b)}$
$=\dfrac{bc.abc}{a^2(b+c)}+\dfrac{ca.abc}{b^2(c+a)}+\dfrac{ab.abc}{c^2(a+b)}$
$=\dfrac{b^2c^2}{a(b+c)}+\dfrac{c^2a^2}{b(c+a)}+\dfrac{a^2b^2}{c(a+b)}$
Đặt $ab=x; bc=y; ca=z$ => xyz=1
=>$Q=\dfrac{y^2}{x+z}+\dfrac{z^2}{x+y}+\dfrac{x^2}{y+z}\ge\dfrac{(x+y+z)^2}{2(x+y+z)}=\dfrac{x+y+z}{2}$
$\ge \dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}$
Dấu = có <=>$ x=y=z=1$ <=> $a=b=c=1$

Bài 9: $P = \dfrac{x}{\sqrt[]{1 - x}} + \dfrac{y}{\sqrt[]{1 - y}} = \dfrac{x}{\sqrt[]{y}} + \dfrac{y}{\sqrt[]{x}}$
$= \dfrac{x^2}{x\sqrt[]{y}} + \dfrac{y^2}{y\sqrt[]{x}} \ge \dfrac{(x + y)^2}{ x\sqrt[]{y} + y\sqrt[]{x}}$ (Theo BĐT Cauchy - Schwazt)
= $\dfrac{1}{\sqrt[]{x} \sqrt[]{xy} + \sqrt[]{y}\sqrt[]{xy}} \ge \dfrac{1}{\sqrt[]{(x + y)(xy + xy)}}$ (Áp dụng BĐT Bunhiacopski ở mẫu)
=$\dfrac{1}{\sqrt[]{2xy}} \ge \dfrac{1}{\sqrt[]{2\dfrac{(x + y)^2}{4}}}$ (Áp dụng BĐT Cô Si ở mẫu)
= $\sqrt[]{2}$
Dấu = có <=> $x = y = \dfrac{1}{2}$

Cách làm tổng quát cho dạng bài 12 (có thể trong trường hợp 2 số, 3 số,.....)
$S = a + b + c + \dfrac{3}{a} + \dfrac{9}{2b} + \dfrac{4}{c}$
$= m(a + 2b + 3c) + (1 - m)a + \dfrac{3}{a} + (1 - m)b + \dfrac{9}{2b} + (1 - m)c + \dfrac{4}{c}$
Áp dụng BĐT Cô Si: $(1 - m)a +\dfrac{3}{a} \ge 2\sqrt[]{3(1 - m)}$
Dấu = có <=> $a = \sqrt[]{\dfrac{3}{1 - m}}$
$(1 - m)b + \dfrac{9}{2b} \ge 2\sqrt[]{9(1 - m)}$
Dấu = có <=> $b = \sqrt[]{\dfrac{9}{2(1 - m)}}$
$ (1 - m)c + \dfrac{4}{c} \ge 2\sqrt[]{4(1 - m)}$
Dấu = có <=> $c = \sqrt[]{\dfrac{4}{1 - m}}$
Cộng theo vế các BĐT trên ta được:
$S \ge 20m + 2\sqrt[]{3(1 - m)} + 2\sqrt[]{9(1 - m)} + 2\sqrt[]{4(1 - m)}$
Vậy ta chỉ cần tìm giá trị m thì bài toán sẽ được giải quyết. Việc tìm m là việc giải PT:
Ta thấy, dấu = có tại $a + 2b + 3c = 20$
<=> $$\sqrt[]{\dfrac{3}{1 - m}} + 2\sqrt[]{\dfrac{9}{2(1 - m)}} + 3\sqrt[]{\dfrac{4}{1 - m}} = 20$$
Trong bài này việc tìm m không khó vì chúng cùng mẫu nên dễ giải. Tuy nhiên ở các bài mà PT đó nhìn có vẻ khó giải thì ta chỉ cần nhập PT vào máy tính rồi nhẩm nghiệm thì ta được m (thường thì m có giá trị là số đẹp) vì cả phần trên chỉ là việc ngoài nháp, khi viết vào bài chỉ cần thay giá trị m vào là được.


Đó là cách mình nghĩ ra trong quá trình làm 1 số bài kiều như vậy. Nếu có gì đó sai sót thì các bạn góp ý thêm

Nhưng mình có cái rất băn khoăn:
Về kỹ thuật biến đổi ( đã tìm được dấu =) thì vẫn thấy nó hơi "mò", vì khi biết dấu = thì có rất nhiều cách biến đổi nhưng vì sao mà có thể tìm được cách đúng để có thể biến đổi biểu thức và áp dụng các bất đẳng thức quen thuộc được? Không lẽ thử từng trường hợp một hay sao??

 

[conga222222]

Nhưng mình có cái rất băn khoăn:
Về kỹ thuật biến đổi ( đã tìm được dấu =) thì vẫn thấy nó hơi "mò", vì khi biết dấu = thì có rất nhiều cách biến đổi nhưng vì sao mà có thể tìm được cách đúng để có thể biến đổi biểu thức và áp dụng các bất đẳng thức quen thuộc được? Không lẽ thử từng trường hợp một hay sao??

chính vì thế thì bất đẳng thức mới khó nếu có một phương pháp chung thì còn khó gì nữa nhưng không hoàn toàn là mò làm nhiều bài tập thì sẽ học được một số hướng chứng minh thường dùng (làm càng nhiều thì số cách chứng minh thu được càng nhiều) khi làm nếu dùng những phương pháp đã biết thì sẽ mò ra được còn nếu gặp bài nào lạ hoắc thì chỉ còn nước giơ cờ đầu hàng thôi
$\eqalign{
& bai\;2 \cr
& dat\;{4^x} = a;\;{4^y} = b;\;{4^z} = c \cr
& \to a,b,c > 0 \cr
& abc = {4^{x + y + z}} = 1 \cr
& \to \sqrt {3 + {4^x}} + \sqrt {3 + {4^y}} + \sqrt {3 + {4^z}} = \sqrt {3 + a} + \sqrt {3 + b} + \sqrt {3 + c} \cr
& \cos i: \cr
& 3 + a = 1 + 1 + 1 + a \geqslant 4\root 4 \of a \cr
& tuong\;tu... \cr
& \to \sqrt {3 + a} + \sqrt {3 + b} + \sqrt {3 + c} \geqslant \sqrt {4\root 4 \of a } + \sqrt {4\root 4 \of b } + \sqrt {4\root 4 \of c } \cr
& \cos i:\sqrt {4\root 4 \of a } + \sqrt {4\root 4 \of b } + \sqrt {4\root 4 \of c } \geqslant 3\root 3 \of {\sqrt {{4^3}\root 4 \of {abc} } } = 6 \cr
& dau = \leftrightarrow ... \cr} $

 

[tthandb]

chính vì thế thì bất đẳng thức mới khó nếu có một phương pháp chung thì còn khó gì nữa nhưng không hoàn toàn là mò làm nhiều bài tập thì sẽ học được một số hướng chứng minh thường dùng (làm càng nhiều thì số cách chứng minh thu được càng nhiều) khi làm nếu dùng những phương pháp đã biết thì sẽ mò ra được còn nếu gặp bài nào lạ hoắc thì chỉ còn nước giơ cờ đầu hàng thôi

Thi toán cũng cần thêm yếu tố may mắn nữa nhỉ :-SS:-SS:-SS

 

[tthandb]

chính vì thế thì bất đẳng thức mới khó nếu có một phương pháp chung thì còn khó gì nữa nhưng không hoàn toàn là mò làm nhiều bài tập thì sẽ học được một số hướng chứng minh thường dùng (làm càng nhiều thì số cách chứng minh thu được càng nhiều) khi làm nếu dùng những phương pháp đã biết thì sẽ mò ra được còn nếu gặp bài nào lạ hoắc thì chỉ còn nước giơ cờ đầu hàng thôi

 

[baihocquygia]

đội 7

Bài 12
Ta có
S= (3a/4+3/a) + ( c/4+4/c) + (b/2+9/2b) + a/4 + b/2 + 3c/a \geq 2.[TEX]\sqrt{9/4}[/TEX] +2.[TEX]\sqrt{1}[/TEX]+2.[TEX]\sqrt{9/4}[/TEX] +(a+2b+3c)/4 \geq 13
Dấu bằng xảy ra khi a=2,b=3,c=4

 

[letsmile519]

Đội 4:

Bài 6:

$(u^2+\frac{1}{u^2})^2+(v^2+\frac{1}{v^2})^2$=$4+u^4+v^4+\frac{1}{v^4}+\frac{1}{u^4}$\geq$4+u^4+v^4+\frac{1}{v^4}+\frac{1}{u^4}$\geq $4+(u^2+v^2)^2/2+\frac{4}{u^2+v^2}=\frac{25}{2}$
dấu = khi $u=v=1/\sqrt[]{2}$
-> đpcm

 

[letsmile519]

Đội 4

Bài 3:

Ta có $\sqrt[]{c-4}.a.b$\leq $\frac{cab}{4}$

$bc.\sqrt[]{a-2}$\leq $\frac{bca}{2\sqrt[]{2}}$

$ca\sqrt[]{b-3}$\leq $\frac{acb}{2\sqrt[]{3}}$

\Rightarrow $P$\leq $\frac{\frac{cab}{4}+\frac{bca}{2\sqrt[]{2}}+\frac{acb}{2\sqrt[]{3}}}{abc}$

-> Max P

 

[letsmile519]

Đội 4:

Bài 5:

a ) $\frac{1}{\sum a^2}+\frac{9}{\sum ab}$\geq $\frac{9}{\sum a^2+2\sum ab}+\frac{7}{\sum ab}$=$\frac{9}{(a+b+c)^2}+\frac{7}{\sum ab}$\geq $9+\frac{7}{\frac{1}{3}}=30$

Dâu = khi $x=y=z=\frac{1}{3}$

b) $\sum \frac{1}{a^2+b^2}+\sum \frac{1}{ab}$\geq $4\sum \frac{1}{(a+b)^2}+\sum \frac{1}{2ab}$\geq $\frac{4}{3}(\sum \frac{1}{a+b})^2+\frac{9}{2(ab+bc+ca)}$\geq $\frac{4}{3}(\frac{9}{2})^2+\frac{9}{\frac{2}{3}}=40.5$


Dâu = khi $x=y=z=\frac{1}{3}$

c)$Q$\geq $\frac{36}{(a+b+c)^2+ab+bc+ca}+\frac{9}{2(ab+bc+ca)}$\geq $\frac{36}{1+\frac{1}{3}}+\frac{9}{\frac{2}{3}}=40.5$

 

[chonhoi110]

đội 3

Bài 10

$\sqrt{x^2+\dfrac{1}{x^2}}.\sqrt{1^2+9^2} \ge x+\dfrac{9}{x}=81x+\dfrac{9}{x}-80x \ge 54-80x$

Tương tự với y,z ~ > $\sqrt{82}.VT=162-80(x+y+z)\ge 82$

Bài 11

$\sum \sqrt{a^2 \underbrace{\dfrac{1}{16b^2}+...\dfrac{1}{16b^2} }_{16}}\ge \sum \sqrt{17\sqrt[17]{a^2.(\dfrac{1}{16b^2})^{16}}}$

$=\sqrt{17}\sum \sqrt[17]{\dfrac{a}{16^8b^{16}}}\ge \sqrt{17} \sqrt[3]{\sqrt[17]{\dfrac{a}{16^8b^{16}}}\sqrt[17]{\dfrac{b}{16^8c^{16}}}\sqrt[17]{\dfrac{c}{16^8a^{16}}}}=3\sqrt{17}\sqrt[17]{\dfrac{1}{16^8a^5b^5c^5}}\ge \dfrac{3\sqrt{17}}{2}$

 

[huynhbachkhoa23]

Bài 2:

Theo Minkovsky hay BDT độ dài, BDT vector gì cũng đúng:

$VT \ge \sqrt{27+(2^x+2^y+2^z)^2} \ge \sqrt{27+9.2^{x+y+z}}=6$

Bài 4:

$VT^3 \le 36(a+b+c)=27 \rightarrow VT \le 3$

Bài 9:

$f(x)=\dfrac{x}{\sqrt{1-x}}$

Tự chứng minh $f(x) \ge \dfrac{3\sqrt{2}}{2}(x-\dfrac{1}{2})+\dfrac{\sqrt{2}}{2}$

Ráp vào.

Bài 10:

Theo Minkovsky:

$VT \ge \sqrt{(\sum x)^2+(\sum \dfrac{1}{x})^2} = \sqrt{81(\sum x)^2+(\sum \dfrac{1}{x})^2-80(\sum x)^2} \ge \sqrt{18(\sum x)(\sum \dfrac{1}{x})-80} \ge \sqrt{82}$

Bài 11:

Tương tự bài 10.

Bài 12:

Hình như cái này dùng Albel thì phải.

 

[huynhbachkhoa23]

Bài 7:

Đặt $x=\dfrac{a}{b}; y=\dfrac{b}{c}; z=\dfrac{c}{a}$

$x,y,z>0; xyz=1$

$A=\dfrac{\sum x^{3/2}}{\sum x} \ge \dfrac{(\sum x)^{3/2}}{\sqrt{3}\sum x}=\dfrac{(\sum x)^{1/2}}{\sqrt{3}} \ge \dfrac{\sqrt{3}\sqrt[4]{xyz}}{\sqrt{3}}=1$