[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Cho uA=uB= 2 cos(20*pi*t-pi/3)
v= 30cm/s, AB=20cm.
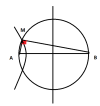
a) Điểm M cực đại thuộc đường tròn đường kính AB. tính MB max
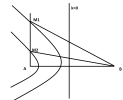
b) Điểm M cực đại sao cho tâm giác MAB vuông tại A. tính MA max, MA min
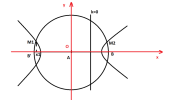
c) Điểm M cực đại thuộc đường tròn tâm A, bán kính AB. Tính MB max, MB min và khoảng cách nhất từ M tới trung trực của AB.
Hi vọng anh chị giúp em với ạ. Em cảm ơn mọi người nhiều
v= 30cm/s, AB=20cm.
a) Điểm M cực đại thuộc đường tròn đường kính AB. tính MB max
b) Điểm M cực đại sao cho tâm giác MAB vuông tại A. tính MA max, MA min
c) Điểm M cực đại thuộc đường tròn tâm A, bán kính AB. Tính MB max, MB min và khoảng cách nhất từ M tới trung trực của AB.
Hi vọng anh chị giúp em với ạ. Em cảm ơn mọi người nhiều